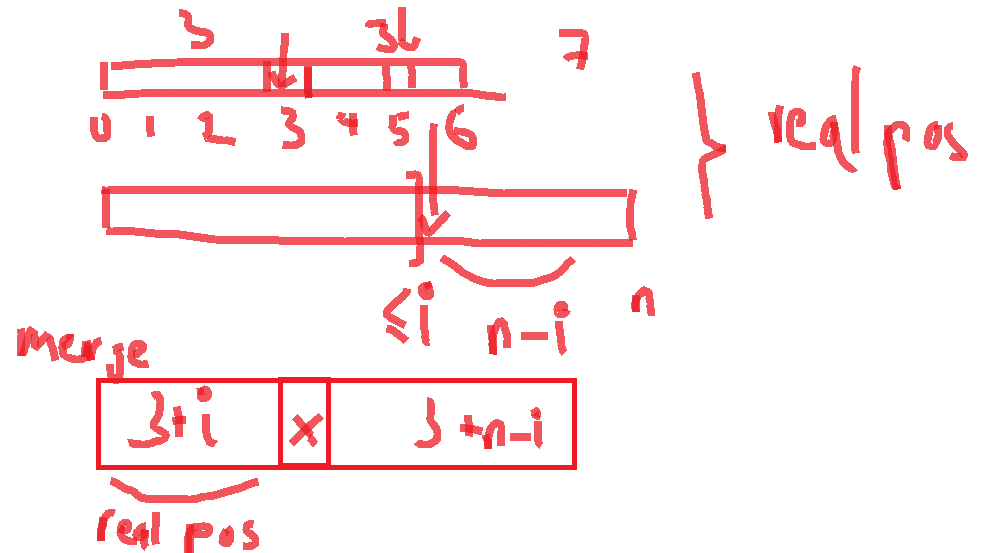4. Median of Two Sorted Arrays

Problem¶

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)).

Example 1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2:

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

Solve¶

Easy mode, merge them and return median¶

O(n log n)

No need to bother making it O(n) using merge, the problem specially said we need a O(log (m+n)) time complexity.

I still leave it like this so at least, I finish the problem.

Runtime 86 ms Beats 79.70%
Memory 16.5 MB Beats 68.59%

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        nums = nums1 + nums2
        nums.sort()
        if len(nums) % 2 == 1:
            return nums[len(nums)//2]
        return (nums[len(nums)//2 - 1] + nums[len(nums)//2] ) / 2.

Hard mode, binary search all the way we go¶

White board¶

Let say we deal with nums1 length m, and nums2 array with length n.

I can try each number x in nums1 (or nums2), try to find it’s real position after merge both array
- We know x position in nums1 (which mean it cost O(1))
- We can try find position of x in nums2 using binary search (cost us O(log m))
- So the “find x’s real position” cost me O(log m) time
We also know that x is in a sorted array, so x[i] < x[i+1] < ... and also mean x[i]’s real position in merged array also increasing.
- We need to find the median position, which mean we need to find x[i] that have it’s real position = median position of merged array = (n+m)/2
- Case (n+m) % 2 == 0 (even length merged array), we also need to find (n+m)/2 - 1 position element in merged array.
- By what we analyze, we can use binary search to check on each x[i] in nums1, find take it real position, then base on the x[i] real position vs median position (n+m)/2 we can round down left and right search range range
- So we have a nested log(n) and log(m), meaning try to find a x[i] with real position == median position cost us O(log (n+m)) time complexity
This need to address that, we try only numbers in nums1 array. Median position could be in nums2 array, so we need to run this again on nums2. This is a separated run so we still have O(log (n+m)) time complexity

Implementation - Bisect, Binary search twice¶

O(log (n + m))

I done exactly using what I describe in the write board session

Try to find in nums1:
- A nums1[found] position which have real position (n+m)/2 in merged array
- If total length of merged array (n+m) % 2 == 0 (even length), I rerun binary search again to find nums1[found2] position which have real position (n+m)/2 - 1 in merged array.
- If we can’t find any found or found2, we set it default as -1
Done the same thing with nums2 array, but storing result in found3, found4
If I done it right:
- A odd length merged array will have nums1[found] or nums2[found3] contain the median
- A even length merged array will have (nums1[found] or nums2[found3]) and (nums1[found2] or nums2[found4]) contain the median.
- Calculate result base on which one contain value (which mean found != -1)

Note - Some real pain I have is that:

I repeat the search function in if total % 2 == 0: part, where I not set l, r = -1, m, which have me a Runtime error submit.
I not follow binary search formal while loop expression, which I forgot to add l != r - 1, which make me have another Runtime error submit on empty list.
I forgot/unanalyzed the problem deep enough so that I not handle case where nums1[i] = x is in nums2 array, which make x can have a possible range of position in the merged array. This make me have a Wrong answer submit.
I also forgot and try to find mid instead of nums1[mid] in nums2, this not cause me any problem tho.

Final implementation have it runtime slower than O(n log n) solution, which is fair when we using python

Runtime 111 ms Beats 6.8%
Memory 16.6 MB Beats 35.48%

class Solution:

    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:

        def binary_search(nums1, nums2):
            m = len(nums1) 
            n = len(nums2)
            total = m + n
            found = -1
            found2 = -1
            l, r = -1, m
            while found == -1 and l != r - 1:
                mid = (l + r) // 2
                pos = bisect_right(nums2,nums1[mid])
                posLeft = bisect_left(nums2,nums1[mid])
                realPos = mid + pos
                possiblePos = mid + posLeft

                if possiblePos <= total // 2 <= realPos :
                    found = mid
                elif realPos < total // 2:
                    l = mid
                else:
                    r = mid
                if l == r-1:
                    break
            if total % 2 == 0:
                l, r = -1, m
                while found2 == -1 and l != r - 1:
                    mid = (l + r) // 2
                    pos = bisect_right(nums2,nums1[mid])
                    posLeft = bisect_left(nums2,nums1[mid])
                    realPos = mid + pos
                    possiblePos = mid + posLeft

                    if possiblePos <= total // 2 - 1 <= realPos :
                        found2 = mid
                    elif realPos < total // 2 - 1:
                        l = mid
                    else:
                        r = mid
                    if l == r-1:
                        # print(realPos, l, r, nums1[l])
                        break
            # print(found, found2)
            return (found, found2)

        found, found2 = binary_search(nums1, nums2)
        found3, found4 = binary_search(nums2, nums1)
        res = 0
        if found != -1:
            res += nums1[found]
        elif found3 != -1:
            res += nums2[found3]
        if found2 != -1:
            res += nums1[found2]
            res = res / 2.
        elif found4 != -1:
            res += nums2[found4]
            res = res / 2.

        return res

Reimplementation - C lang and pain with binary search¶

O(log (m+n))

I want to know is this actually better than normal O(n):

I don’t have built-in binary search (bisect in python), so I have to implement my own, which I miss judge a lot of time. I have to separated them in two separated function for sanity (Still it do the same thing, I done it right on binary search part)
Ran into runtime error every time as I try to access out of scope index from provided array variable (in python it not throw error but give me some revert value, which need the same amount of debug time on why I get wrong result)
Some needed even more deep understanding of case where nums1[mid] is found in nums2 array. Which require a lot of my debug time.

Final implementation is quite a better score, but after some dig into summited code, I found a lot O(n) implementation have better runtime.

Runtime 7 ms Beats 92.34%
Memory 7.2 MB Beats 6.74%

// If found return 1, else return 0
int binarysearch_right(int* nums, int numsSize, int val) {
    int l = -1;
    int r = numsSize;
    int mid;

    while (l != r -1) {
        mid = (l + r) >> 1;
        if (nums[mid] <= val) 
            l = mid;
        else
            r = mid;
    }
    return l;
}

int binarysearch_left(int* nums, int numsSize, int val) {
    int l = -1;
    int r = numsSize;
    int mid;

    while (l != r -1) {
        mid = (l + r) >> 1;
        if (nums[mid] < val) 
            l = mid;
        else
            r = mid;
    }
    return r;
}

int binarysearch(int* nums, int numsSize, int val, int* leftMost, int* rightMost) {
    *leftMost =  binarysearch_left(nums, numsSize, val);
    *rightMost =  binarysearch_right(nums, numsSize, val);
    return *leftMost <= *rightMost;
}

// Only find using element in nums1, if nums1 not contain mergeArrayPos'th element return -1
int findMergeArrayPos(int* nums1, int nums1Size, int* nums2, int nums2Size, int mergeArrayPos) {
    int l = -1;
    int r = nums1Size;
    int mid, val;
    int pos = -1;

    while (l != r-1) {
        mid = (l + r) >> 1;
        // printf("l=%d, r=%d, mid=%d\n", l, r, mid);

        val = nums1[mid];

        int leftMost, rightMost;
        int isFound = binarysearch(nums2, nums2Size, val, &leftMost, &rightMost);
        int true_position = mid + leftMost;

        if (isFound) {
            int possiblePos = mid + rightMost + 1;
            // printf("Range (left = %d, right %d), need %d\n", true_position, possiblePos, mergeArrayPos);
            if (mergeArrayPos <= possiblePos && true_position <= mergeArrayPos) {
                pos = mid;
                break;
            }
        }

        if ( mergeArrayPos == true_position) {
            pos = mid;
            break;
        }

        if (true_position < mergeArrayPos) {
            l = mid;
        } else if ( mergeArrayPos < true_position ) {
            r = mid;
        } 
    }

    // if (pos != -1) printf("Found mergeNums[%d] = %d\n", mergeArrayPos, nums1[pos]);
    return pos;
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size){
    if (nums2Size == 0) {
        return findMedianSortedArrays(nums2, nums2Size, nums1, nums1Size);
    }
    if (nums1Size == 0) {
        int mid = nums2Size >> 1;
        if (nums2Size % 2 == 0)
            return (nums2[mid] + nums2[mid-1]) / 2.;
        else
            return (double) nums2[mid];
    }

    int total = nums1Size + nums2Size;
    int mergePos = total >> 1;
    double res = 0.;
    // printf("Find pos\n");
    int pos = findMergeArrayPos(nums2, nums2Size, nums1, nums1Size, mergePos);
    if (pos == -1) {
        // printf("Retry find pos\n");
        pos = findMergeArrayPos(nums1, nums1Size, nums2, nums2Size, mergePos);
        res += nums1[pos]; 
    } else {
        res += nums2[pos]; 
    }
    // printf("Find pos2\n");
    if (total % 2 == 0) {
        mergePos -= 1;
        int pos2 = findMergeArrayPos(nums2, nums2Size, nums1, nums1Size, mergePos);
        if (pos2 == -1) {
            // printf("Retry find pos2\n");
            pos2 = findMergeArrayPos(nums1, nums1Size, nums2, nums2Size, mergePos);
            res = (res + nums1[pos2]) /2.; 
        } else {
            res = (res + nums2[pos2]) /2.; 
        }
    }
    // printf("Final result = %f\n", res);
    return res;
}

void testBinarySearch(int* nums1, int nums1Size, int val){
    int leftMost, rightMost;
    int isFound = binarysearch(nums1, nums1Size, val, &leftMost, &rightMost);
    if (isFound) {
        printf("Found %d in range [%d, %d]\n", val, leftMost, rightMost);
    }
    else {
        printf("Not found %d, middle range [%d, %d]\n", val, leftMost, rightMost);
    }
}

One round Binary search - 0ms solution that I yanked¶

TODO, JUST WTH is this code

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size){
    if(nums1Size > nums2Size) {
        return findMedianSortedArrays(nums2, nums2Size, nums1, nums1Size);
    }

    int totalSize = nums1Size + nums2Size;
    int left = 0, right = nums1Size;

    while(left <= right) {
        int part1 = left + (right - left) / 2;
        int part2 = (totalSize + 1) / 2 - part1;

        int maxLeft1 = (part1 == 0) ? INT_MIN : nums1[part1 - 1];
        int minRight1 = (part1 == nums1Size) ? INT_MAX : nums1[part1];

        int maxLeft2 = (part2 == 0) ? INT_MIN : nums2[part2 - 1];
        int minRight2 =(part2 == nums2Size) ? INT_MAX : nums2[part2];

        if(maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {
            if(totalSize % 2 == 0) {
            return (double)(fmax(maxLeft1 ,maxLeft2) + fmin(minRight1, minRight2)) / 2.0;
            } else {
                return (double)fmax(maxLeft1, maxLeft2);
            }
        } else if(maxLeft1 > minRight2) {
            right = part1 - 1;
        } else {
            left = part1 + 1;
        }
    }

    return 0.0;
}

Last update : September 23, 2023
Created : September 23, 2023