Skip to content

84. Largest Rectangle in Histogram

Problem

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

Pasted image 20230817235856.png

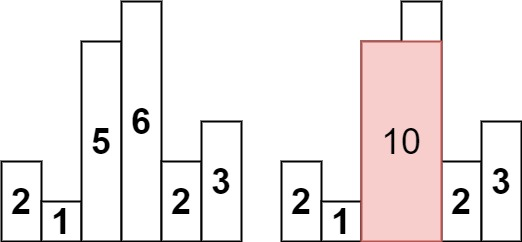
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Constraints:

  • 1 <= heights.length <= 10**5
  • 0 <= heights[i] <= 10**4

Solve

Cache it all

O(n ** 2)

We need what information, we cache it:

  • Loop through the provided height array from left to right ([0..n])
  • Using a dictionary hash map cache to store all the rectangle we can create up until now
  • Calculate the next one using: cache[(i,p)] = cache[(i-1,p)] + p which mean:
    • With current bar with a height of p ;
    • we can append it and form a rectangle to the last know i-1 index p height rectangle.
from collections import defaultdict

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        cache = defaultdict(int)
        largest = 0 
        for i, h in enumerate(heights):
            for p in range(1, h+1):
                cache[(i,p)] = cache[(i-1,p)] + p
                if largest < cache[(i,p)]:
                    largest = cache[(i,p)]

        return largest

Optimize

O(n ** 2 log n)

  • Binary search: Using binary search instead of loop through all possible p in [0..h] with each bar; only calculating and caching p with a clear know of it
  • Optimize memory: We only need index (i-1) information to process index i, so we don’t need to cache/can free any thing before it.
  • Optimize calculation: We only need to store the appearance of each height, check for largest rectangle only when it goes out of the scope or end of the loop.
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        cache = [{}, {}]
        prev, curr = 0, 1
        largest = 0 

        for i, h in enumerate(heights):
            if i == 0:
                h = heights[0]
                cache[prev][h] = i
                largest = h
                prev_keys = [h]
                continue

            insert_pos = bisect_right(prev_keys, h)
            curr_keys = prev_keys[:insert_pos].copy()

            for key in prev_keys[:insert_pos]:
                cache[curr][key] = cache[prev][key]

            if h not in prev_keys:
                cache[curr][h] = i
                if insert_pos < len(prev_keys):
                    cache[curr][h] = cache[prev][prev_keys[insert_pos]]
                curr_keys.append(h)

            for key in prev_keys[insert_pos:]:
                if largest < (i-cache[prev][key])*key:
                    largest = (i-cache[prev][key])*key

            curr, prev = prev, curr
            prev_keys = curr_keys
            # print(cache[curr])
            cache[curr] = {}

        for key in cache[prev]:
            if largest < (len(heights)-cache[prev][key])*key:
                largest = (len(heights)-cache[prev][key])*key
        return largest
  • Try to clear the dictionary and using copy for quickly create key array, I quite gave up at this point
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        cache = [[], [|], []]
        prev, curr = 0, 1
        largest = 0 
        prev_keys = []

        for i, h in enumerate(heights):
            if i == 0:
                h = heights[0]
                largest = h
                cache[prev].append(i)
                prev_keys = [h]
                continue

            insert_pos = bisect_right(prev_keys, h)
            curr_keys = prev_keys[:insert_pos].copy()
            cache[curr] = cache[prev][:insert_pos].copy()

            if h not in prev_keys:
                curr_keys.append(h)
                cache[curr].append(i)
                if insert_pos < len(prev_keys):
                    cache[curr][-1] = cache[prev][insert_pos]

            for k, start in enumerate(cache[prev][insert_pos:]):
                key = insert_pos + k 
                if largest < (i-start)*prev_keys[key]:
                    largest = (i-start)*prev_keys[key]

            curr, prev = prev, curr
            prev_keys = curr_keys
            # print(cache[curr])

        for i, key in enumerate(cache[prev]):
            if largest < (len(heights)-key)*prev_keys[i]:
                largest = (len(heights)-key)*prev_keys[i]
        return largest

After understand the yanked code, I realize a lot more imprisonment window:

  • We not need separated prev and curr cache. We can just reuse the prev one directly, pop out any unused <out of the scope> rectangle
  • So I only use cache and keys, instead of having curr_keys, prev_keys, curr, prev, cache[curr] = cache[prev]
  • We used the previous keys array directly, so instead of use bisect_right to find the cut out, calculate the <out of the scope> rectangle first and update using a while loop pop() them out until the height of the last one in keys array is lower than current processed height h.
    • This also mean we have to find another way to get the cache[prev][insert_pos], which is a product of bisect_right and already be free from memory by keys.pop(). so I set a term w and update it every time using keys.pop()
  • We also can append a [0] at the end so we can reused the logic inside the loop to find largest rectangle, instead of using separated loop at the end.

O(n ** 2)

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        cache = []
        keys = []
        largest = 0

        for i, h in enumerate(heights + [0]):
            if i == 0:
                h = heights[0]
                largest = h
                cache.append(i)
                keys.append(h)
                continue

            w = i
            while len(keys) > 0 and keys[-1] > h:
                k = keys.pop()
                start = cache.pop()
                if largest < (i-start)*k:
                    largest = (i-start)*k
                w = start

            if len(keys) == 0 or keys[-1] != h:
                keys.append(h)
                cache.append(w)

        return largest

Gave up: Yank some code

This is quite close to final version of mine some how

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        if len(heights) == 1:
            return heights[0]
        # stack = [<remember_height>, <window_length>]]
        stack = [[heights[0], 1|heights[0], 1]]
        topHeight, topWidth = stack[-1]
        largest = heights[0]

        for h in heights[1:] + [0]:
            w = 1
            if stack and h <= topHeight:
                while stack and h < topHeight:
                    currH, currW = stack.pop()
                    topHeight, topWidth = stack[-1] if stack else (None, None)
                    w += currW
                    area = (w - 1) * currH
                    if area > largest:
                        largest = area
                if stack and h == topHeight:
                    topWidth += w
                    stack[-1] = (h, topWidth)
                    continue
            topHeight, topWidth = h, w
            stack.append((topHeight, topWidth))
        return largest

Last update : September 17, 2023
Created : August 16, 2023