134. Gas Station

Problem¶

There are n gas stations along a circular route, where the amount of gas at the ith station is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from the ith station to its next (i + 1)th station. You begin the journey with an empty tank at one of the gas stations.

Given two integer arrays gas and cost, return the starting gas station’s index if you can travel around the circuit once in the clockwise direction, otherwise return -1. If there exists a solution, it is guaranteed to be unique

Example 1:

Input: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
Output: 3
Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

Example 2:

Input: gas = [2,3,4], cost = [3,4,3]
Output: -1
Explanation:
You can’t start at station 0 or 1, as there is not enough gas to travel to the next station.
Let’s start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can’t travel around the circuit once no matter where you start.

Constraints:

• n == gas.length == cost.length
• 1 <= n <= 105
• 0 <= gas[i], cost[i] <= 104

Solve¶

White board¶

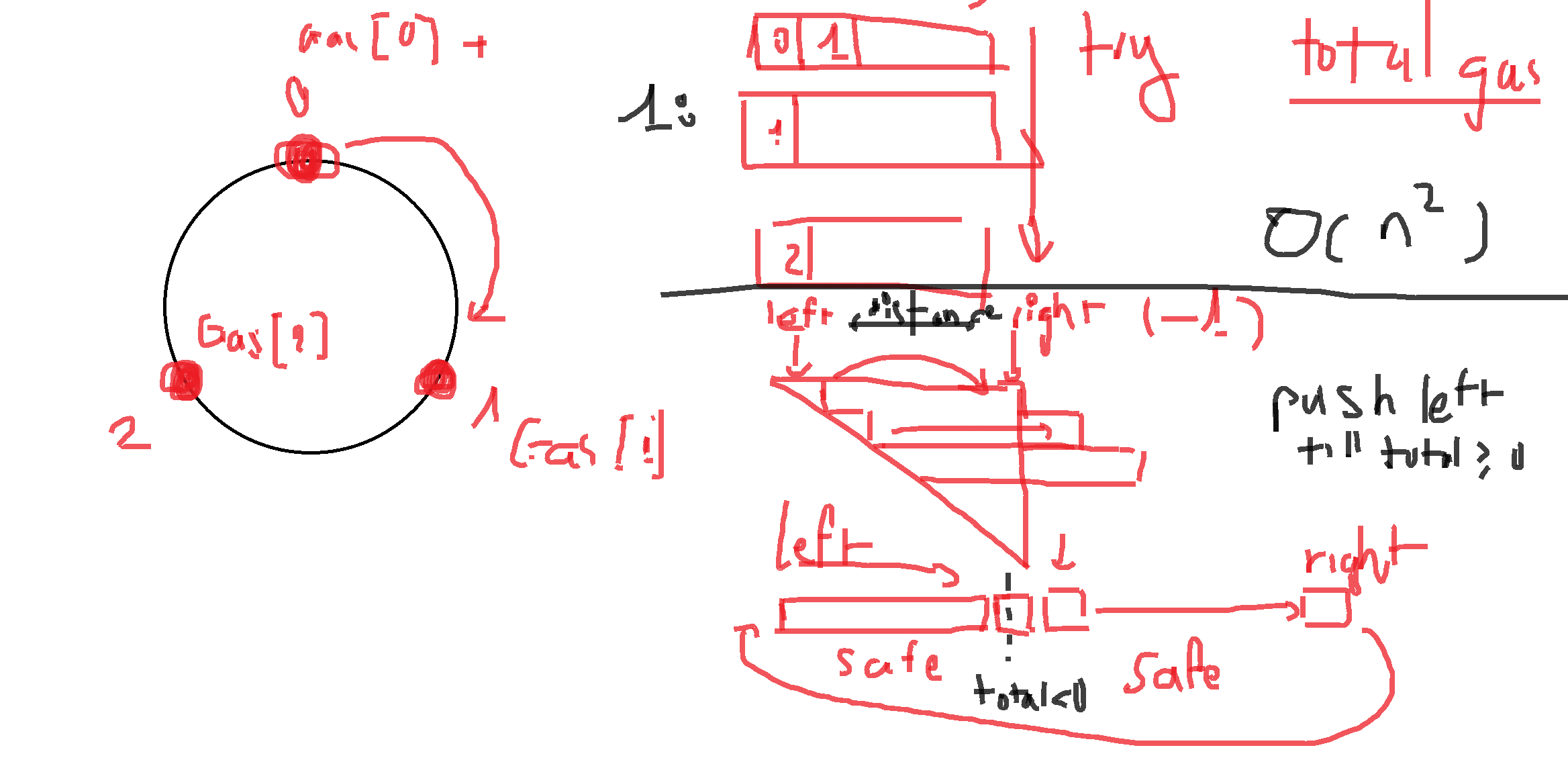
Here I see two 2 option:

1. A quick O(n ** 2) case:
   Which we try on each start point, and simulating the running car (oblivious case)
2. Try to kept the result (caching):
   • It hard to reuse the calculated path, if we ever try to reused, a space needed in worst case could be O(n ** 2). Here I could try pre-calculate sum gas[0..i] and cost[0..i]. But, again, it seem not that ideal using that could help solve the problem
   • The next one I think it could be better is a sliding window on a recursive list
     • Start with left = right = 0
     • When the window reach length = n, or | left - right | = n we can stop and return left
     • While Increasing right, if the total of sliding window total < 0, we increasing left till total >= 0
     • This mean, if the ever left > n, we have try all possible start point, thus we can’t found a solution and return -1

Attempt on flow chart

Implementation 1 : O(n ** 2) trying it all¶

O(n ** 2)

• Still, even a easy thing could go wrong, it cost me quite some times to implement this some how ??

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        n = len(gas)
        for i in range(n):
            total_gas = gas[i] - cost[i]
            if total_gas < 0:
                continue
            check = True
            # print (f"gas: {total_gas}, at gas[{i}]")

            for j in range(1,n+1):
                nextGas = i + j
                nextGas %= n
                nextCost = cost[nextGas]
                nextGas = gas[nextGas]
                total_gas = total_gas + nextGas - nextCost
                # print (f"gas: {total_gas}, at gas[{(i + j) % n}]")
                if total_gas < 0:
                    check = False
                    break
            if check:
                return i
        return -1

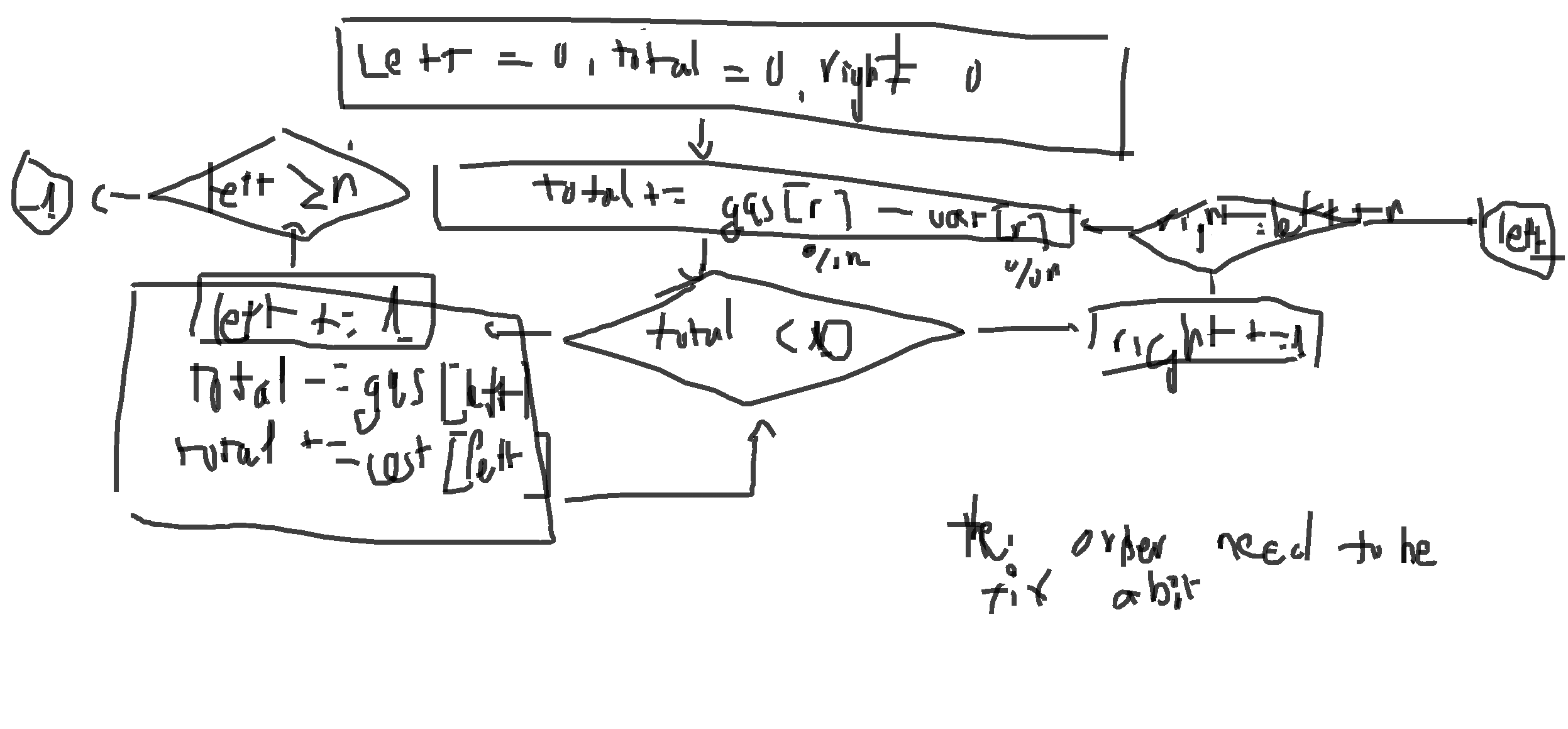
Sliding window¶

O(n)

Python¶

• The flow chart is actually right, which is nice
• right can only travel 2n, left can only travel n, while it is nested, both is independent, making this a O(n) times complexity

Still, the result isn’t that great at all ? Here is final implementation

1141ms
Beats 22.82% of users with Python3

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        n = len(gas)
        total = left = right = 0
        while right < left + n:
            total += gas[right % n] - cost[right % n]
            while total < 0:
                total -= gas[left] - cost[left]
                left += 1
                if left >= n:
                    return -1
            right += 1

        return left

Any other language implementation¶

This make me feel like try on a different language, again, every one beat me some how while using C

127ms
Beats 53.02% of users with C

c

int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
    int n = costSize;
    int total = 0;
    int left = 0;
    int right = 0;

    while (right < left + n) {
        total += gas[right % n] - cost[right % n];

        while (total < 0){
            total -= gas[left] - cost[left];
            left += 1;            
            if (left >= n) {
                return -1;
            }
        }
        right += 1;
    }
    return left;
}

Still, Leetcode C calculating result implementation is slow (too much over head) i think, let try another, use rust this time. It still slower than a lot of people here ?
rust

12ms
Beats 69.15% of users with Rust

impl Solution {
    pub fn can_complete_circuit(gas: Vec<i32>, cost: Vec<i32>) -> i32 {
        let n = gas.len();
        let mut total = 0;
        let mut left = 0;
        let mut right = 0;

        while right < left + n {
            total += gas[right % n] - cost[right % n];
            while total < 0 {
                total -= gas[left] - cost[left];

                left += 1;
                if left >= n {
                    return -1;
                }
            }
            right += 1;
        }

        left as i32
    }
}

Still, why?? - Yank and read the code¶

O(n)

Here is the best code possible in rust (5ms)

• First it seem just add all gas and cost, enumerate it, result (idx, diff)
• Wrapping a Fold to make a accumulator tuple on 3 variable: (total_gas, current_gas, start)
• Loop through all index and (idx, diff) with key control flow:
  • current_gas < 0 work just like total of our sliding window, and instead of increasing left by one each, we just need to jump to index+1 (~ right+1 in my implement) here it seem (?)
  • It not even need to calculate anything above O(n). The total_gas is obliviously the total of our sliding window if we ever found a result. Which if it < 0, making it a invalid result and we return -1
• By all of this, return the final total accumulation on all gas[i] - cost[i], and start value.

For my thought, this have a lot of assuming and reasoning behind that we could ever use this type of return result. We are seem trying to:

• Combine our right := left -> left + n accumulation loop
• With our left updating loop skip -> Just jump to index + 1 and set total to 0
• With reducing the need to recalculating total_gas

This all cost quite some time to analyzing and isn’t seem to be possible with my current knowledge

Resubmit the same code, result is worse than my implementation. This make me think that Leetcode is just in heavy load, and my implementation is good enough

15ms
Beats 44.68% of users with Rust

impl Solution {
    pub fn can_complete_circuit(gas: Vec<i32>, cost: Vec<i32>) -> i32 {
        assert!(gas.len() > 0);
        assert_eq!(gas.len(), cost.len());

        let (total, _, start) = gas
            .into_iter()
            .zip(cost.into_iter())
            .map(|(gas, cost)| gas - cost)
            .enumerate()
            .fold(
                (0, 0, 0),
                |(mut total_gas, mut current_gas, mut start), (idx, diff)| {
                    total_gas += diff;
                    current_gas += diff;
                    if current_gas < 0 {
                        current_gas = 0;
                        start = idx + 1;
                    }

                    (total_gas, current_gas, start)
                },
            );

        if total >= 0 {
            start as i32
        } else {
            -1
        }
    }
}