148. Sort List

Problem¶

Given the head of a linked list, return the list after sorting it in ascending order.

Example 1:

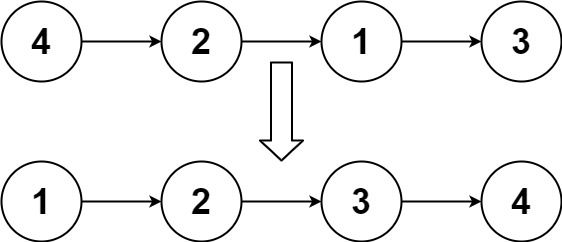
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

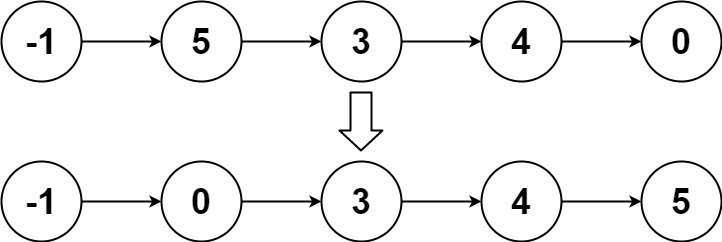
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]

Example 3:

Input: head = []
Output: []

Constraints:

• The number of nodes in the list is in the range [0, 5 * 104].
• -105 <= Node.val <= 105

Follow up: Can you sort the linked list in O(n logn) time and O(1) memory (i.e. constant space)?

Solve¶

Quick thought and white board¶

O(1) memory could mean using in-place sorting this seem not that possible for any O(n log n). Still, I think could try using merge sort here, this make possible as we dealing with linked list, which it self have some ideal way of memory handling.

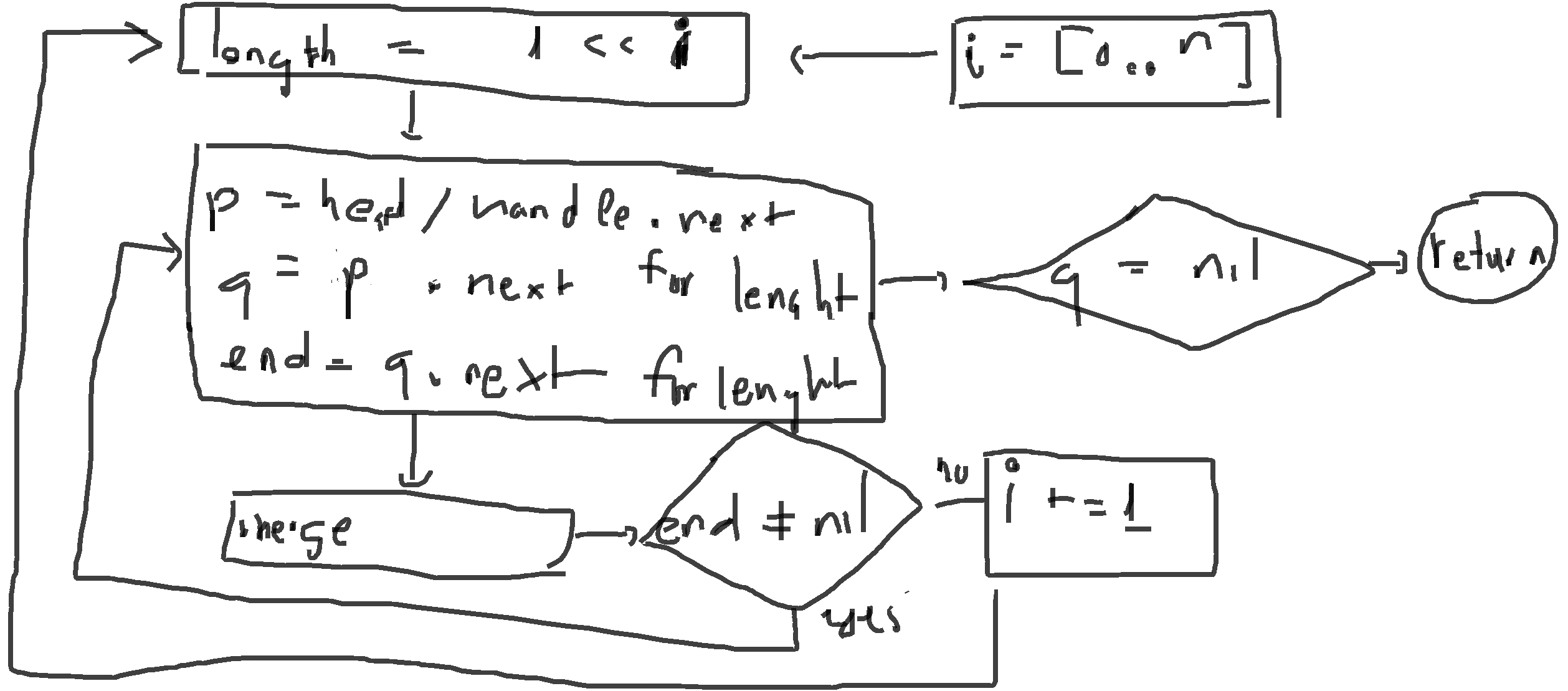
Quick though on merge sort with bottom up appoarch

Flow chart attempt

Merge sort is quite a complex thing to do a flow chart

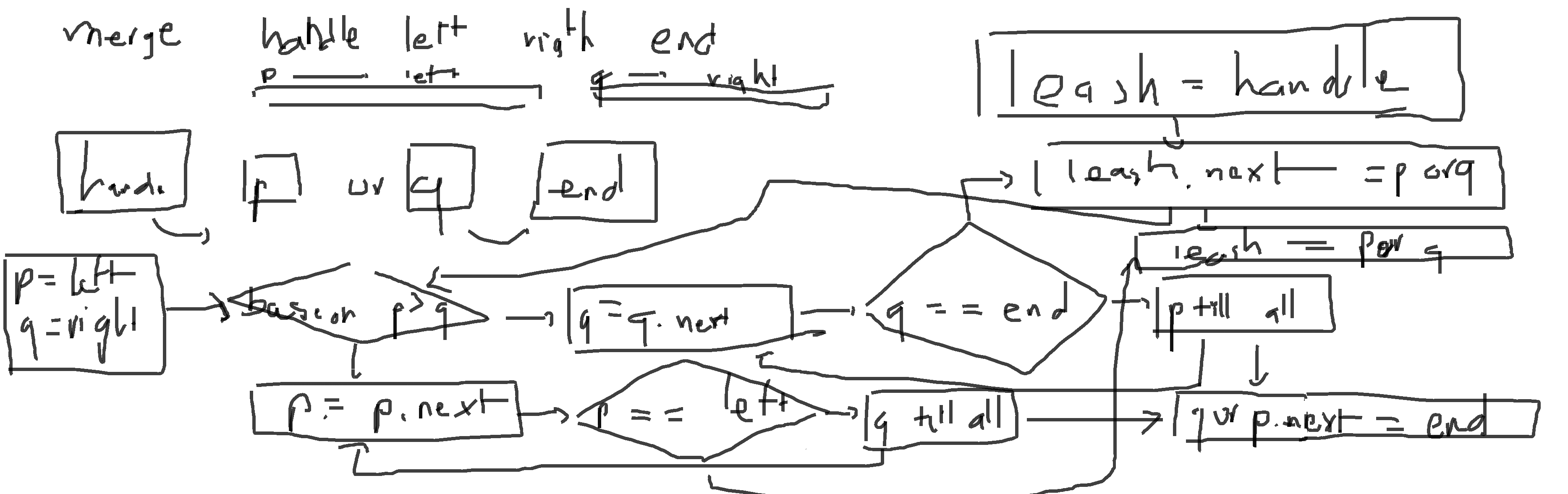
Implementation Merge sort bottom up¶

This is hard, a really hard way to do a simple thing, while the result is just too bad in python.

Doing it in O(1) space

My flow chart is garbage here, but let talk about it:

• First, we want to split the linked list. This can be done using Bottom up or Top down approach, which here I using bottom up:
  • This is done by split them into a length = 2 ** i = 1 << i , or length in [1, 2, 4, 8, ...]
  • If this adding up to the length of the inputted linked list, we are done merging
  • If the linked list isn’t being traversal all the way yet, this mean we can split it to at least two linked array. So, we have to merge it
  • This mean, we trying to merge two linked list length ~ length together
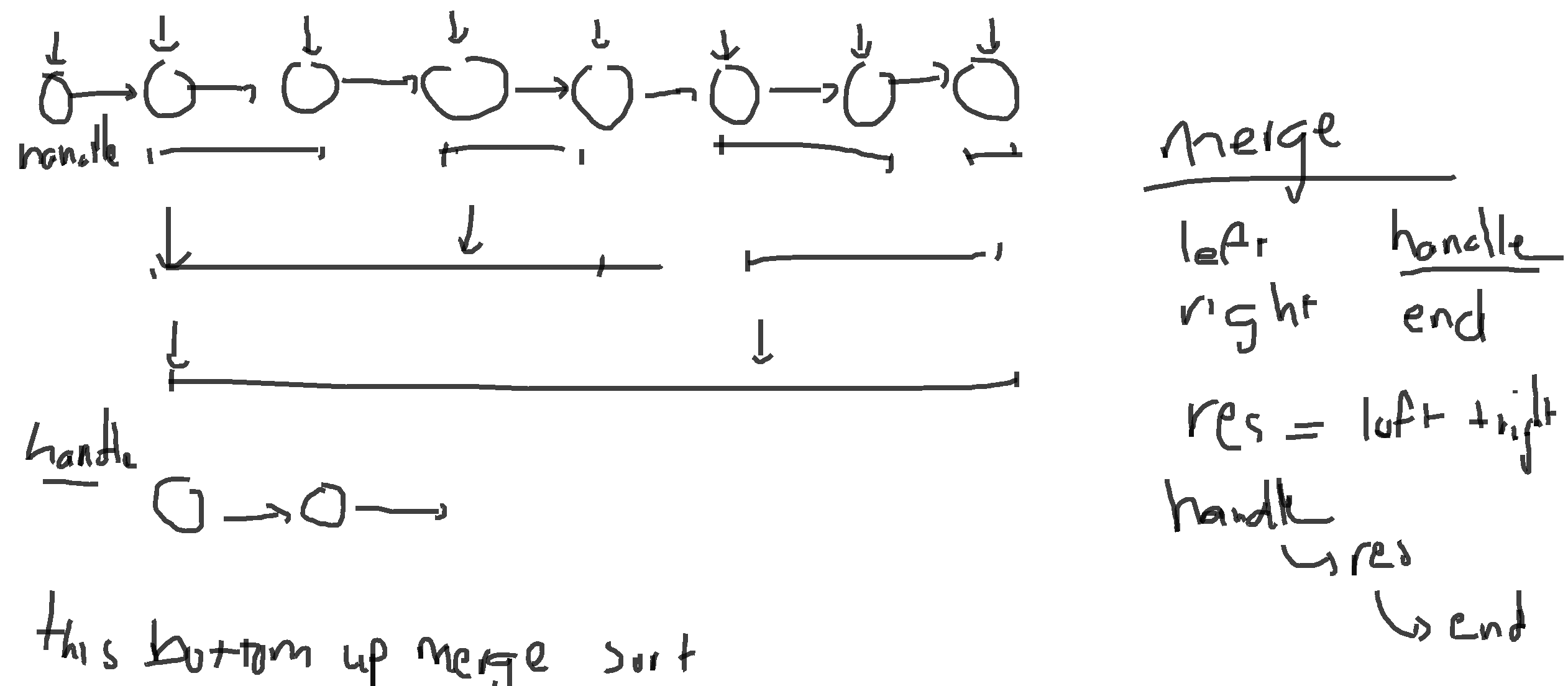
• Merge Sort isn’t a big of a deal, but we need at least 4 input:
  • Start : This is the handle of the Linked list, which isn’t in the merge range (or sorted range) and remain unchanged. This require so that we can keep the linked list flow in right order. We should have Start = prev_Left
  • Left: This is the head of First list, The first list should be Left -> ... -> prev_Right
  • Right: This is the head of Second list, which should be Right -> ... -> prev_End
  • End: Similar to start, but it out side merge range and at the end.
  • We done the merge part by:
    • Start with leash = Start, p start from start of the first linked list Left, q start from start of the second linked list Right.
    • Link it to either p or q base on their value, minimum have higher piority.
      • If either reach their corresponded end (p == Right or q == End), we push all remain p or q into leash
    • The last leash is linked to End
    • To help our next merge, we return the leash which is the next start point of the next merge (if had)
• This mean, we have to handle the main loop to extract and call merge sort on all needed for input (start, left, right, end)
  • To simplify the problem, I create a temp handle that connect to head of inputted linked list, this mean case where left = head can have start = handle
  • We can loop through the linked list once, each time keep track of start, left, right, end:
    • If we have left == head, right == None, end == None, this mean we done merge and the linked list is sorted
    • If we have left != head, right == None, end == None, this mean we can skip the merge function and go to next length
    • If we have right != None, we try to reach till end:
      • We need to merge founded start, left, right, end
      • If end == None, which mean we not have any remain node to merge, so we go to the next length

Here, I just please my self if I have some extra way to contain split point, like a array or some thing similar, but oh well.

645ms
Beats 14.82% of users with Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:

    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:

        def merge(start, left, right, end):
            leash = start
            p = left
            q = right
            while True:
                if p != right and q != end:
                    if p.val < q.val:
                        leash.next = p
                        leash = leash.next
                        p = p.next
                    else:
                        leash.next = q
                        leash = leash.next
                        q = q.next
                elif p != right:
                    leash.next = p
                    leash = leash.next
                    p = p.next
                elif q != end:
                    leash.next = q
                    leash = leash.next
                    q = q.next
                elif p == right and q == end:
                    break
                # print(leash.val)
            leash.next = end
            return leash

        handle = ListNode(0, head)
        for i in range(4 * 4 * 4 * 4):
            length = 1 << i
            start = handle
            end = None
            while True:
                p = start.next
                q = p
                for _ in range(length):
                    if q == None:
                        if p == handle.next:
                            return handle.next
                        else:
                            break
                    q = q.next

                if q == None:
                    break
                end = q
                for _ in range(length):
                    if end == None:
                        break
                    end = end.next

                prev_end = merge(start, p, q, end)
                # print(handle, start.val, p.val, q.val, end == None)
                if end != None:
                    start = prev_end
                else:
                    break
        return handle.next

Obvious way is just delinked list and sort the whole thing in one go, but this is fine.
I don’t think this code is unreadable, but it quite hard to implement.

This mean, I should care more about the approach before decide to code the thing. Let see some easier approach, while of course using some thing that rewarded than python.

Top down Merge sort¶

O(n log n)

• Well, top down is even harder, you want to split the list in half. Every single time.

TBH I taking longer to finish this, but overall the code look easier to understand that the bottom up approach
- The main point is that we split it into actual Linked list, rather than keeping it inplace
- This reduce the need of start and end variable

• Now, the merge sort just need to received a single linked list as input. Split it in half, sort each half, then merge it
• For the split, we split them into two real linked list (link end of left and right into NIL or 0)
  • Split could use two pointer to find the middle Node.
  • A prev_p is used to track the end of left linked list, so we can set prev_p -> next = 0 to split left into a different linked list.
• Other than that, the main merge flow work the same.
  • We still need temp value to hold the head of new list. Which is temp.next here, I use a stack allocate temp variable so that I not need to free that address after finishing the function.
  • Return the head temp.next of new list so that after merge old head could have been move to other place merge

67ms
Beats 61.63% of users with C

/**

 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


typedef struct ListNode Node;

// void printLinkedList(Node* head) {
//     Node* p = head;
//     while (p != 0) {
//         printf("%d ", p->val);
//         p = p->next;
//     }
//     printf("\n");
// }

void split_half (Node* head, Node** left, Node** right) {
    if (head == 0) {
        *left = 0;
        *right = 0;
        return;
    }
    Node *prev_p = 0;
    Node *p = head;
    Node *q = head;
    while (true) {
        prev_p = p;
        p = p->next;
        q = q->next;
        if (q == 0)
            break;
        q = q->next;
        if (q == 0)
            break;
    }
    *left = head;
    prev_p->next = 0;
    *right = p;
}

Node* merge_sort(Node* head) {
    if (head == 0 || head->next == 0) {
        return head;
    }
    Node temp;
    Node* leash = &temp; 

    Node* left, *right;
    split_half(head, &left, &right);
    // if (left != 0) printLinkedList(left);
    // if (right != 0) printLinkedList(right);
    // printf("\n");
    left = merge_sort(left);
    right = merge_sort(right);
    Node* p = left;
    Node* q = right;
    while (true) {
        if (p != 0 && q != 0) {
            if (p->val < q->val) {
                leash->next = p;
                leash = leash->next;
                p = p->next;
            } else {
                leash->next = q;
                leash = leash->next;
                q = q->next;
            }
        } else if (p != 0) {
            leash->next = p;
            leash = leash->next;
            p = p->next;
        } else if (q != 0) {
            leash->next = q;
            leash = leash->next;
            q = q->next;
        } else if (p == 0 && q == 0) {
            break;
        }
    }

    // printLinkedList(temp.next);
    return temp.next;
}

struct ListNode* sortList(struct ListNode* head){
    Node* prev, *left, *right, *start, *end;
    Node* p = head;
    head = merge_sort(head);
    return head;
}

Rust ?¶

We not even have a mutable value, which mean, we can’t change the input

impl Solution {
    pub fn sort_list(head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {
        match &mut head {
            Some(node) => {
                node.val = 5;
                return head;
            }
            None => {
                return head;
            }
        }
    }
}

Thus require us, to modify provided function into a mutable one

impl Solution {
    pub fn sort_list(mut head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {

        match &mut head {
            Some(node) => {
                node.val = 5;
                return head;
            }
            None => {
                return head;
            }
        }
    }
}

Now this is some what workable, but overall, isn’t even ideal for this type of question. Hmmmmmmmmm ? Guess I never know.