212. Word Search II
Problem¶
Given an m x n board of characters and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example 1:
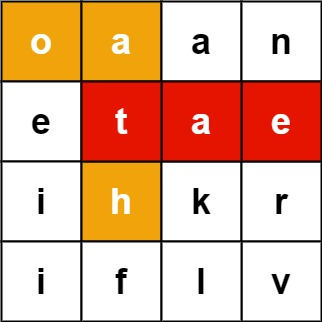
Input: board = [[“o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”|”o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”]], words = [“oath”,”pea”,”eat”,”rain”]
Output: [“eat”,”oath”]
Example 2:
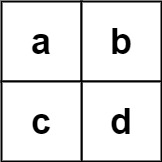
Input: board = [[“a”,”b”],[“c”,”d”|”a”,”b”],[“c”,”d”]], words = [“abcb”]
Output: []
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]is a lowercase English letter.1 <= words.length <= 3 * 1041 <= words[i].length <= 10words[i]consists of lowercase English letters.- All the strings of
wordsare unique.
Solve¶
DP but fail one¶
python
This just throw TLE a lot on me
Guess just BFS/DFS is good enough.
I finding all possible available appearance of every string, storing they head, and tail, and all the path in between in a cache dictionary.
To make the storing a bit simpler and lower the memory for storing need, I only store string with length that is a power of 2 (2**n length), all words is split to the similar length [1, 2, 4, 8, ...] and check in cache before being process.
def split(self,w):
splitRes = []
clone = w
p = len(w)
i = 0
while p>0:
q = (p & 1) << i
if q:
splitRes.append(clone[:q])
clone = clone[q:]
i += 1
p >>= 1
return splitRes
def find(self, w, board, cache):
sw = self.split(w)
knowedPath = None
for s in sw:
print(s)
paths = self.findPaths(s, cache)
if len(paths) == 0:
return False
if knowedPath is None:
knowedPath = paths
continue
res = self.combine(knowedPath, paths)
if len(res) == 0:
return False
knowedPath = res
cache[w] = knowedPath
return True
I do it in top-down, so that if it hit cache, then we can return directly, or else we split it again, but in half. This return all available, possible path that string s appear on the board.
def findPaths(self, s, cache):
print("+",s)
if s in cache:
return cache[s]
if len(s) == 1:
return []
p1 = self.findPaths(s[:len(s)//2], cache)
p2 = self.findPaths(s[len(s)//2:], cache)
cache[s] = self.combine(p1, p2)
return cache[s]
The combine is where I take the path check for intersection, and the continuation of the head, tail of both path.
Final implement can be really fast, but going bad when the total possible path goes out of hand.
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/26/2023 07:29 | Time Limit Exceeded | N/A | N/A | python3 |
class Solution:
def split(self,w):
splitRes = []
clone = w
p = len(w)
i = 0
while p>0:
q = (p & 1) << i
if q:
splitRes.append(clone[:q])
clone = clone[q:]
i += 1
p >>= 1
return splitRes
def isadj(self, tk, hp):
if abs(tk[0] - hp[0]) == 1:
return tk[1] == hp[1]
if abs(tk[1] - hp[1]) == 1:
return tk[0] == hp[0]
return False
def combine(self, ks, ps):
res = []
for k, hk, tk in ks:
for p, hp, tp in ps:
if k.isdisjoint(p) and self.isadj(tk, hp):
res.append((k.union(p), hk, tp))
return res
def findPaths(self, s, cache):
print("+",s)
if s in cache:
return cache[s]
if len(s) == 1:
return []
p1 = self.findPaths(s[:len(s)//2], cache)
p2 = self.findPaths(s[len(s)//2:], cache)
cache[s] = self.combine(p1, p2)
return cache[s]
def find(self, w, board, cache):
sw = self.split(w)
knowedPath = None
for s in sw:
print(s)
paths = self.findPaths(s, cache)
if len(paths) == 0:
return False
if knowedPath is None:
knowedPath = paths
continue
res = self.combine(knowedPath, paths)
if len(res) == 0:
return False
knowedPath = res
cache[w] = knowedPath
return True
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
cache = {}
for r, row in enumerate(board):
for i, c in enumerate(row):
if c not in cache:
cache[c] = []
path = set()
path.add((r,i))
head = (r,i)
tail = (r,i)
cache[c].append((path, head, tail))
res = []
for w in words:
print('==',w)
if self.find(w, board, cache):
res.append(w)
return res
Fallback 1000¶
python
So, in case we have of a lot possible path, this give a fall back needed to process the problem. Just process the first 1000 possible path, if it can’t solve the problem, going with the full join
While this barely can finish the problem, but Leetcode do a add up in TLE calculating (They send all the test as one input, after certain time, you get a TLE), which mean I pass the TLE case, but leaving me no time left to easier case.
class Solution:
def split(self,w):
splitRes = []
clone = w
p = len(w)
i = 0
while p>0:
q = (p & 1) << i
if q:
splitRes.append(clone[:q])
clone = clone[q:]
i += 1
p >>= 1
return splitRes
def isadj(self, tk, hp):
if abs(tk[0] - hp[0]) == 1:
return tk[1] == hp[1]
if abs(tk[1] - hp[1]) == 1:
return tk[0] == hp[0]
return False
def combine(self, ks, ps):
res = []
for k, hk, tk in ks:
for p, hp, tp in ps:
if k.isdisjoint(p) and self.isadj(tk, hp):
res.append((k.union(p), hk, tp))
return res[:1000]
def combineFull(self, ks, ps):
res = []
for k, hk, tk in ks:
for p, hp, tp in ps:
if k.isdisjoint(p) and self.isadj(tk, hp):
res.append((k.union(p), hk, tp))
return res
def findPaths(self, s, cache):
# print("+",s)
if s in cache and (s in self.isFull):
return cache[s][:1000]
if len(s) == 1:
return []
p1 = self.findPaths(s[:len(s)//2], cache)
p2 = self.findPaths(s[len(s)//2:], cache)
cache[s] = self.combine(p1[:1000], p2[:1000])
if len(cache[s]) == 0 and (len(p1) == 1000) or (len(p2) == 1000):
cache[s] = self.findPathsFull(s, cache)
return cache[s][:1000]
def findPathsFull(self, s, cache):
# print("+ full",s)
if (s in cache) and (s in self.isFull):
return cache[s]
if len(s) == 1:
return []
self.isFull.add(s)
p1 = self.findPathsFull(s[:len(s)//2], cache)
p2 = self.findPathsFull(s[len(s)//2:], cache)
cache[s] = self.combineFull(p1, p2)
return cache[s]
def find(self, w, board, cache):
sw = self.split(w)
knowedPath = None
for s in sw:
# print(s)
paths = self.findPaths(s, cache)
if len(paths) == 0:
return False
if knowedPath is None:
knowedPath = paths
continue
res = self.combine(knowedPath, paths)
if len(res) == 0:
return False
knowedPath = res
cache[w] = knowedPath
return True
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
cache = {}
self.isFull = set()
for r, row in enumerate(board):
for i, c in enumerate(row):
if c not in cache:
cache[c] = []
path = set()
path.add((r,i))
head = (r,i)
tail = (r,i)
cache[c].append((path, head, tail))
self.isFull.add(c)
res = []
for w in words:
# print('==',w)
if self.find(w, board, cache):
res.append(w)
return res
What we missing¶
1 <= words.length <= 3 * 10**41 <= words[i].length <= 10
This meaning we need to do a lot of small words length. Then the split seem isn’t do that much as we do a rather small string
We will want to reuse path a lot more. with a more precision combine, as we only do combine on self.isadj(tk, hp), which it self can be added to cache instead of checking boardly. So maybe, I need to use some of the head, tail as a cache input to make this a possible solution.
Yank it, Trie tree solution¶
python
Read and learn¶
There is some Trie Tree that you need to learn and finish this problem? Maybe, but I try and fail on DP, so let have some basic reading this code:
- We create a
TrieNodehelper class/object that havechildrento cache store all possible path goes through; a end of word flag for what ever? - We then have Trie, the main object, which split word into similar set of character. This mean when we get our self into a spiting node, we can reused the path up to that spiting point as a similarity
- Which also mean, any path in the Trie tree that can’t be found on the
boardwe can skip processing them.
While this is a fine use case, it doesn’t help with a repetitive case where there just too many path.
class TrieNode:
def __init__(self):
self.children = {}
self.endOfWord = False
class Trie:
def __init__(self,total_words):
self.root = TrieNode()
self.unfound_words = total_words
def insert(self, word: str) -> None:
cur = self.root
for c in word:
if c not in cur.children:
cur.children[c] = TrieNode()
cur = cur.children[c]
cur.endOfWord = True
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
res = []
M , N = len(board) , len(board[0])
d = Trie(len(words))
for w in words:
d.insert(w)
…Fast for ward to the main solve function
A helper function go, that:
- Take a position
(r,c), check for current word stages, basically like a BFS, and curr_node that keeping up with the Trie tree
def go(r,c,s,cur_node):
if cur_node.endOfWord:
res.append(s)
cur_node.endOfWord = False
d.unfound_words -= 1
if d.unfound_words == 0:
return
if r < 0 or c < 0 or r >= M or c >= N:
return
cur_chr = board[r][c]
if cur_chr not in cur_node.children:
return
cur_root = cur_node
cur_node = cur_node.children[cur_chr]
board[r][c] = '69'
go(r+1,c,s+cur_chr,cur_node)
go(r-1,c,s+cur_chr,cur_node)
go(r,c-1,s+cur_chr,cur_node)
go(r,c+1,s+cur_chr,cur_node)
board[r][c] = cur_chr
if not cur_node.children:
del cur_root.children[cur_chr]
return
- And the main just going into the board one cell by one cell and do BFS on every cell
root = d.root
for i in range(M):
for j in range(N):
if d.unfound_words == 0:
return res
go(i,j,"",root)
return res
So key take away is that we process all the words, at once, on each cell of the board. This make the process easier and stop the process if there isn’t any path can lead to words.
Re-implement¶
The yank implement does seem great, so I keep that in mind and start implement
The first is Trie tree, which I use ["!"] element to store the word, also keeping track of it parent so that I can cut down some of the TreeNode.
class TrieNode:
def __init__(self, above = None):
self.above = above
self.char = {}
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, w):
p = self.root
for c in w:
if c not in p.char:
p.char[c] = TrieNode(p)
p = p.char[c]
p.char["!"] = w
def remove(self, w):
p = self.root
s = ""
for c in w:
if c in p.char:
p = p.char[c]
s += c
for c in s[::-1]:
if not p.char:
del p.above.char[c]
else:
break
p = p.above
I also do some pretty printing for debug
def __str__(self):
import json
p = self.root
def helper(p):
d = {}
if p is None:
return d
for k in p.char:
if k == "!":
d[k] = p.char["!"]
continue
d[k] = helper(p.char[k])
return d
return json.dumps(helper(p), indent = 4)
In the main function, I use a visited hash map to keep track of already pass through cell. Get DSP and BFS wrong naming here (This is DFS)
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
tree = Trie()
res = []
visited = set()
for w in words:
tree.insert(w)
m = len(board)
n = len(board[0])
def adj(i,j):
res = []
for x, y in [(i-1,j), (i+1, j), (i, j-1), (i, j+1)]:
if 0 <= x < m and 0 <= y < n and (x,y) not in visited:
res.append((x,y))
return res
def bfs(i,j, node):
visited.add((i,j))
if "!" in node.char:
res.append(node.char["!"])
del node.char["!"]
tree.remove(res[-1])
for x, y in adj(i,j):
c = board[x][y]
if c in node.char:
bfs(x,y, node.char[c])
visited.remove((i,j))
for i, r in enumerate(board):
for j, char in enumerate(r):
if char in tree.root.char:
bfs(i,j, tree.root.char[char])
return res
The final implementation look like this.
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/26/2023 12:49 | Accepted | 1039 ms | 21.8 MB | python3 |
class TrieNode:
def __init__(self, above = None):
self.above = above
self.char = {}
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, w):
p = self.root
for c in w:
if c not in p.char:
p.char[c] = TrieNode(p)
p = p.char[c]
p.char["!"] = w
def remove(self, w):
p = self.root
s = ""
for c in w:
if c in p.char:
p = p.char[c]
s += c
for c in s[::-1]:
if not p.char:
del p.above.char[c]
else:
break
p = p.above
def __str__(self):
import json
p = self.root
def helper(p):
d = {}
if p is None:
return d
for k in p.char:
if k == "!":
d[k] = p.char["!"]
continue
d[k] = helper(p.char[k])
return d
return json.dumps(helper(p), indent = 4)
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
tree = Trie()
res = []
visited = set()
for w in words:
tree.insert(w)
m = len(board)
n = len(board[0])
def adj(i,j):
res = []
for x, y in [(i-1,j), (i+1, j), (i, j-1), (i, j+1)]:
if 0 <= x < m and 0 <= y < n and (x,y) not in visited:
res.append((x,y))
return res
def bfs(i,j, node):
visited.add((i,j))
if "!" in node.char:
res.append(node.char["!"])
del node.char["!"]
tree.remove(res[-1])
for x, y in adj(i,j):
c = board[x][y]
if c in node.char:
bfs(x,y, node.char[c])
visited.remove((i,j))
for i, r in enumerate(board):
for j, char in enumerate(r):
if char in tree.root.char:
bfs(i,j, tree.root.char[char])
return res
Created : August 26, 2023