392. Is Subsequence
Problem¶
Given two strings s and t, return true if s is a subsequence of t, or false otherwise.
A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).
Example 1:
Input: s = “abc”, t = “ahbgdc”
Output: true
Example 2:
Input: s = “axc”, t = “ahbgdc”
Output: false
Constraints:
0 <= s.length <= 1000 <= t.length <= 10**4sandtconsist only of lowercase English letters.
Follow up: Suppose there are lots of incoming s, say s1, s2, ..., sk where k >= 10**9, and you want to check one by one to see if t has its subsequence. In this scenario, how would you change your code?
Solve¶
Find s in t using a straight line Trie-tree¶
O(n)
I like the follow up question, we create a Trie tree using all possible s (s1, s2, …, sk) that need to be check.
But we only have one s here, so the Trie tree from all possible s is a single one line tree.
Let set some number:
- m = t.length
- n = s.length
With out any follow up, this cost O(m) time in worst case
For follow up time complexity, we cost:
- O(k * n) to create Trie-tree for all possible S
- A query to find all s1,s2 … sk is in t could cost us a traversal cost O(length t) + update tree cost O(all tree node) <= O(k * n)
- So overall we could reach O(k * n) + O(m) time complexityBut k = 10 ** 9 ? So we dealing with a 100_000_000_000 low case English character input ~ 100 GB of input here.
O(k * n)isn’t a great solution at all
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
x = 0
i = 0
while x < len(s) and i < len(t):
if t[i] == s[x]:
x += 1
i += 1
return x == len(s)
Trie-tree using t¶
Normal Trie-tree¶
If we in the case that s is random, we couldn’t create Trie-tree on s at all.
This mean, a normal approach is that we preprocess t to a Trie-tree to quickly traversing and finding s.
Now look at 0 <= t.length <= 10 ** 4. This Trie-tree could support 0 <= s.length <= 100, which mean it only need 100 node deep. Also, s and t consist only of lowercase English letters. We could possibility reach \(27^{100}\) possible node for our t Trie-tree.
So, is there a way for this Trie-tree to happened in a limited memory? We have some calculation here
- Assuming we have a maximum input with t = repeat(“qwertyuiopasdfghjklzxcvbnm”, \(\frac{10^4}{27} = 370\)) , which make it possible to have all 100 combination of low case English letter
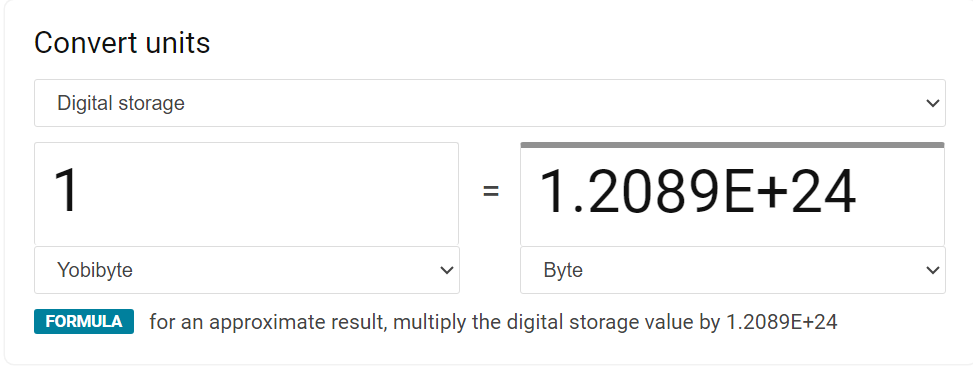
- I could try bitmask to contain 27 letter in a 32 bit variable. But we still deal with nested 100 times number here, making it 32 ** 100 bit length variable = 4 ** 100 byte length ~ 1.60693804E60 byte
- So not that much possible route, unless we have \(10^{36}\) 1 Yobibyte hard drive
But wait, we could use a more friendly pre-calculated search table¶
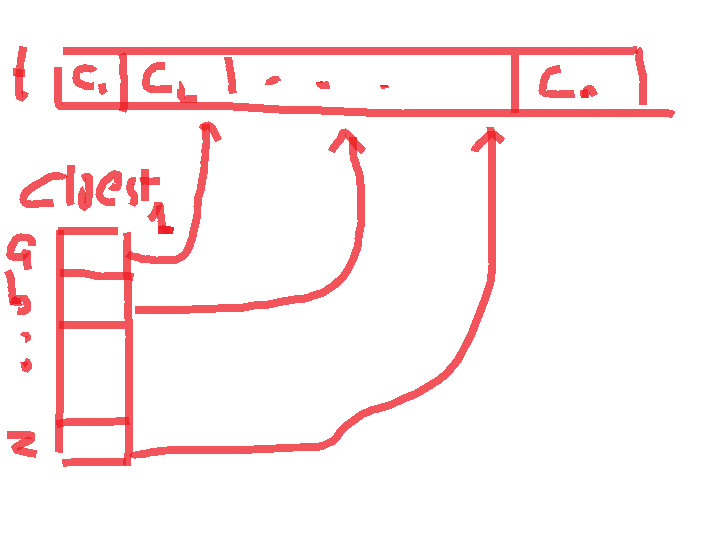
White board¶
On each position, we could have a jump table that point us to the closest position that have corresponded character in t array.
- This way, start from t = 1, we can quickly jump to next position without spending much time in traversal.
- The memory cost is just O(n) or in real number 27 * n memory, which is a possible number.
Implementation - Still with a single s¶
O(n)
- For easy of mind, I use a
dicthere (as we use python). For other language it better a array using char byte code or some “map” implementation for lower memory usage. - The jumpTable create process can be push out side and only need to be created once. In fact here is the first implementation
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
jumpTable = [0] * (len(t)+1)
jumpTable[len(t)] = {}
for index in range(len(t)-1,-1,-1):
c = t[index]
jumpTable[index] = jumpTable[index+1].copy()
jumpTable[index][c] = index + 1
index = 0
for c in s:
if c in jumpTable[index]:
index = jumpTable[index][c]
else:
return False
return True
Here is a cached one, this have a O(m * total test case) space and O(m) time complexity. But if we hit cache, this cost us O(n) to process any s string
class Solution:
def __init__(self):
self.cache = {}
def isSubsequence(self, s: str, t: str) -> bool:
if t in self.cache:
jumpTable = self.cache[t]
else:
jumpTable = [0] * (len(t)+1)
jumpTable[len(t)] = {}
for index in range(len(t)-1,-1,-1):
c = t[index]
jumpTable[index] = jumpTable[index+1].copy()
jumpTable[index][c] = index + 1
index = 0
for c in s:
if c in jumpTable[index]:
index = jumpTable[index][c]
else:
return False
return True
For the follow up, if we hit cache every time with t, then this is a O(k * n) time complexity
Is there a possible under 1s instance answer for the follow up¶
Sample take on how big our data is¶
I try to recreating the Follow up problem using random in go
- The generation it self take for ever ~ 100GB data. Our program take ~ 1_000_000
isSubsequenceon a randomswith sametalready cost us ~ 2s. - This mean it at least take 2 * 100 ~ 200s (without any thing about actual time to real all the data from a hard drive (we are cheating using random here, as every thing happen on RAM, which is way better ?? could be not)
package main
import (
"fmt"
"math/rand"
"sync"
"time"
)
type Solution struct {
cache []([27]int)
mu sync.Mutex
}
func NewSolution() *Solution {
return &Solution{
cache: nil,
}
}
func (sol *Solution) isSubsequence(s, t string) bool {
sol.mu.Lock()
sol.mu.Unlock()
if sol.cache == nil {
println("Not hit cache")
var jumpTable []([27]int)
jumpTable = make([]([27]int), len(t)+1)
for j := 0; j < 27; j++ {
jumpTable[len(t)][j] = -1
}
for i := len(t) - 1; i >= 0; i-- {
c := t[i]
for j := 0; j < 27; j++ {
jumpTable[i][j] = jumpTable[i+1][j]
}
jumpTable[i][c-'a'] = i }
sol.cache = jumpTable
}
jumpTable := sol.cache
idx := 0
for i := 0; i < len(s); i++ {
c := s[i] - 'a'
if jumpTable[idx][c] != -1 {
idx = jumpTable[idx][c]
} else {
return false
}
}
return true
}
func printTime(totaltime time.Duration) {
fmt.Printf("ArrayList test done in: %s\n", totaltime)
}
func main() {
tlength := rand.Intn(10000)
k := rand.Intn(100_000_000)
t := ""
for i := 0; i < tlength; i++ {
t += string(rand.Intn(26) + 'a')
}
sol := NewSolution()
totaltime := time.Duration(0)
printTime(totaltime)
for test := 0; test < k; test++ {
slength := rand.Intn(100)
s := ""
for i := 0; i < slength; i++ {
s += string(rand.Intn(26) + 'a')
}
start := time.Now()
sol.isSubsequence(s, t)
totaltime += time.Now().Sub(start)
if test%1_000_000 == 0 {
fmt.Print(test, " ")
printTime(totaltime)
}
}
}
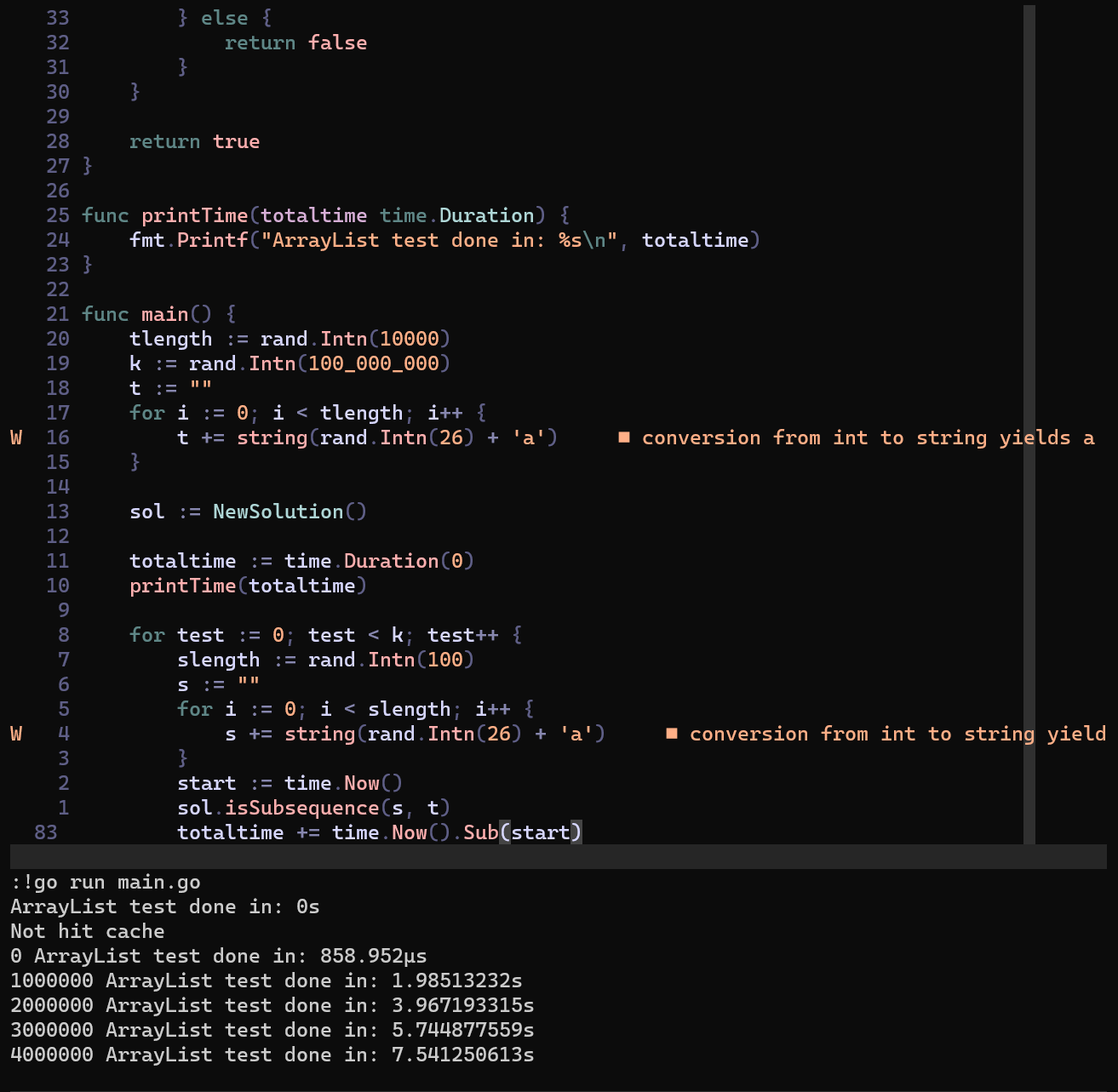
:!go run main.go
ArrayList test done in: 0s
Not hit cache
0 ArrayList test done in: 858.952µs
1000000 ArrayList test done in: 1.98513232s
2000000 ArrayList test done in: 3.967193315s
3000000 ArrayList test done in: 5.744877559s
4000000 ArrayList test done in: 7.541250613s
5000000 ArrayList test done in: 9.292042639s
6000000 ArrayList test done in: 11.054827099s
7000000 ArrayList test done in: 12.835661416s
8000000 ArrayList test done in: 14.608895735s
9000000 ArrayList test done in: 16.384117858s
10000000 ArrayList test done in: 18.155957301s
11000000 ArrayList test done in: 19.921745103s
12000000 ArrayList test done in: 21.688529897s
13000000 ArrayList test done in: 23.463260279s
14000000 ArrayList test done in: 25.181089262s
15000000 ArrayList test done in: 26.945275018s
16000000 ArrayList test done in: 28.705861143s
17000000 ArrayList test done in: 30.470886634s
18000000 ArrayList test done in: 32.240849648s
19000000 ArrayList test done in: 34.003729898s
20000000 ArrayList test done in: 35.767147924s
21000000 ArrayList test done in: 37.525652805s
22000000 ArrayList test done in: 39.295043816s
23000000 ArrayList test done in: 41.069771644s
24000000 ArrayList test done in: 42.827812319s
25000000 ArrayList test done in: 44.603073036s
26000000 ArrayList test done in: 46.363041885s
27000000 ArrayList test done in: 48.130955398s
28000000 ArrayList test done in: 49.887741317s
29000000 ArrayList test done in: 51.69819038s
30000000 ArrayList test done in: 53.627217453s
31000000 ArrayList test done in: 55.414755583s
32000000 ArrayList test done in: 57.195232059s
33000000 ArrayList test done in: 58.982188626s
34000000 ArrayList test done in: 1m0.743219154s
35000000 ArrayList test done in: 1m2.662217948s
36000000 ArrayList test done in: 1m4.53088834s
37000000 ArrayList test done in: 1m6.302977071s
38000000 ArrayList test done in: 1m8.034657804s
39000000 ArrayList test done in: 1m9.859265521s
...
Optimizing 1 - Thread/Goroutine/Multi-core distributed computing¶
I think we isn’t find an possible solution here, but, at least we can make it faster using parallels thread on multi core CPU (I have 8 core in my VM).
- We only need to create one jumpTable
- jumpTable remain unchanged, we only need to read jumpTable in each input
s - This make it possible for multi thread accessing
jumpTableas a constant read memory.
Optimizing 2 - O(Log(n)) for finding S¶
Optimizing 3 - O(1) for finding S ???¶
Created : September 23, 2023