Skip to content

542. 01 Matrix

Problem

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

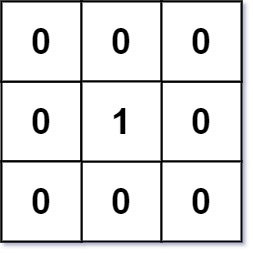
Example 1:

Pasted image 20230817214253.png

Input: mat = [[0,0,0],[0,1,0],[0,0,0|0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0|0,0,0],[0,1,0],[0,0,0]]

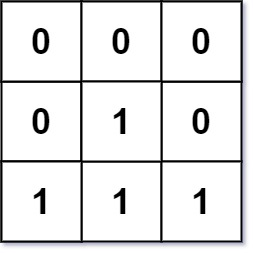
Example 2:

Pasted image 20230817214312.png

Input: mat = [[0,0,0],[0,1,0],[1,1,1|0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1|0,0,0],[0,1,0],[1,2,1]]

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 10**4
  • 1 <= m * n <= 10**4
  • mat[i][j] is either 0 or 1.
  • There is at least one 0 in mat.

Solve

BFS on matrix

python

We consider the matrix as a graph, where a cell of the matrix is <node> in graph

There are a lot of graph problem like this on matrix (or any other form), my general approach is build a helper getAdj(<node>) function that return all adj-nodes of current node (x, y).

We then adding all the cell <node> = (x,y) that have value mat[x][y] == 0 to our queue queue, adding step = 0 to each and start BFS from there.

Still, In bellow implementation when adding the first loop, I also process to have BFS queue start at step 1, all the result is store in cache matrix array (where mat[x][y] == 0 => cache[x][y] == 0)

Time Submitted Status Runtime Memory Language
08/17/2023 21:29 Accepted 630 ms 20.2 MB python3 
class Solution:
    def getAdj(x, y, m,n):
        t = [(x-1, y), (x, y - 1), (x+1, y) , (x, y + 1)]
        res = []
        for i, j in t:
            if 0 <= i < m and 0 <= j < n:
                res.append((i,j))
        return res

    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m = len(mat)
        n = len(mat[0])
        cache = [[-1] * n for _ in range(m)]
        queue = []
        visited = [[False] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if mat[i][j] != 0:
                    continue
                cache[i][j] = 0
                visited[i][j] = True
                adj = Solution.getAdj(i,j, m,n)
                for ai, aj in adj:
                    if mat[ai][aj] != 0 and not visited[ai][aj]:
                        queue.append((ai, aj, 1))
                        visited[ai][aj] = True

        while len(queue) > 0:
            i, j, step = queue.pop(0)
            cache[i][j] = step
            adj = Solution.getAdj(i,j, m,n)
            for ai, aj in adj:
                if not visited[ai][aj]:
                    queue.append((ai, aj, step + 1))
                    visited[ai][aj] = True

        return cache
Last update : September 17, 2023
Created : August 18, 2023