799. Champagne Tower
Problem¶
We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the jth glass in the ith row is (both i and j are 0-indexed.)
Example 1:
Input: poured = 1, query_row = 1, query_glass = 1
Output: 0.00000
Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
Example 2:
Input: poured = 2, query_row = 1, query_glass = 1
Output: 0.50000
Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
Example 3:
Input: poured = 100000009, query_row = 33, query_glass = 17
Output: 1.00000
Constraints:
0 <= poured <= 1090 <= query_glass <= query_row < 100
Solve¶
White board¶
The problem doesn’t explain it self that thoroughly
pouredcan be easily explaining, the total amount of champagne (measure by cup)-
The
query_row, query_glass:- We have the top glass (started glass) is index at
(0, 0), which the information is provided in Example 1 - This mean row of glass have index as
0 - A specific row
idxwithnglass, being index from0 .. n-1
- We have the top glass (started glass) is index at
-
The first thing in my mind is that we simulating the process of pouring champagne (We using code directly here)
- I think it is quite trouble some with
0index or0poured champagne amount, so, I just skip this by some edge case handling before going to main solve function
- Start at row 1, pouring into top glass, we have a
simulation_rowhaving only one glass, I assuming the cup haveinfcapacity, this make it easier to storing stage of each glass and simulating overflow champagne drop to bellow glass:
- We then simulating the process on each row until reach the
query_row
for row in range(query_row): length += 1 new_row = [0. for _ in range(length)] for i in range(length): if i > 0: new_row[i] += (max(simulation_row[i-1] - 1, 0.))/2 if i < length-1: new_row[i] += (max(simulation_row[i] - 1, 0.))/2 simulation_row = new_row if verbose: print(simulation_row)- What we have is that new glass row have length equal to previous row length + 1 (1 more glass), the
length += 1andnew_row = [0. for _ in range(length)]simulating the new added glass row - Now each new glass is being poured into by the overflow champagne of top row:
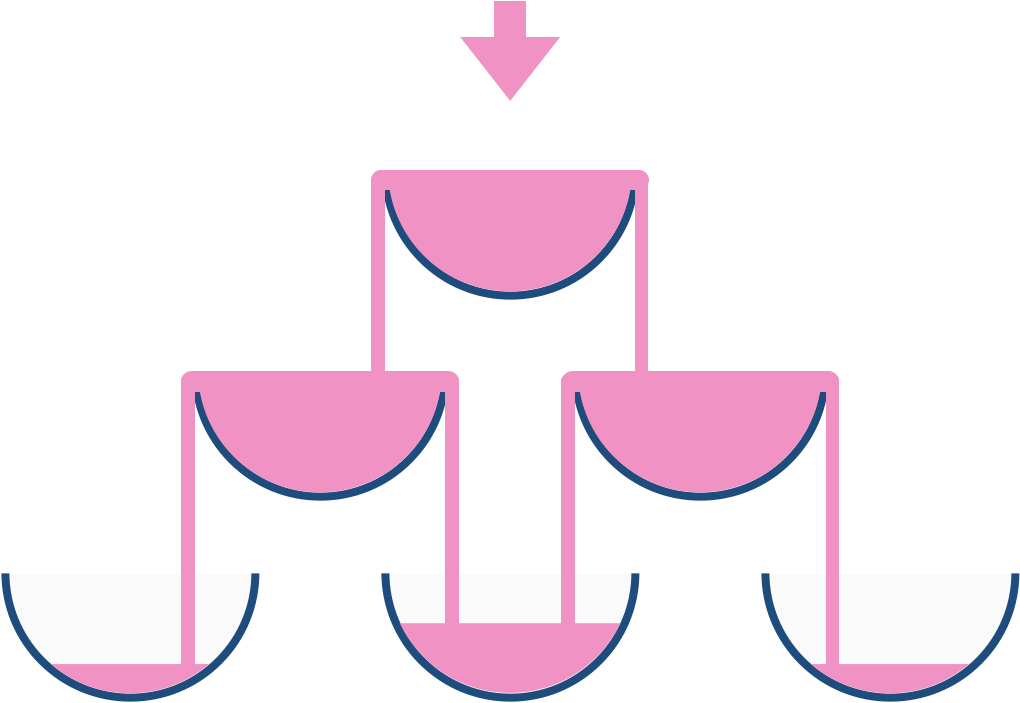
- We can see that, a glass on top row can poured into two glass in the bellow row. Or in reverse, a bellow row glass can be poured by two top row glass (except those in the edge, only being poured by one top glass) so here is the simulation code of the process:
- We need to make sure we leave at least
1.amount of the champagne if we get a overflow case. The overflow amount is dividend into two even amount to two glass bellow, thus we have/ 2in the formula. - Or not giving champagne to the below row if the top row champagne amount is less than
1. - All of that leave we this simulation code
- We need to make sure we leave at least
- The final thing we do is that carry on the
new_rowas ourcurrent_rowand keep processing until we reachquery_rowandquery_glass
- What we have is that new glass row have length equal to previous row length + 1 (1 more glass), the
- I think it is quite trouble some with
The drafted white board code is here: With a time complexity of ~ O(query_row * query_row)
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 09/24/2023 10:52 | Accepted | 152 ms | 16.4 MB | python3 |
class Solution:
def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:
verbose : bool = False
if poured == 0:
return 0.
if poured == 1:
if query_row == 0:
assert query_glass == 0
return 1.
else:
return 0.
simulation_row = [poured * 1.]
length = 1
if verbose: print(simulation_row)
for row in range(query_row):
length += 1
new_row = [0. for _ in range(length)]
for i in range(length):
if i > 0:
new_row[i] += (max(simulation_row[i-1] - 1, 0.))/2
if i < length-1:
new_row[i] += (max(simulation_row[i] - 1, 0.))/2
simulation_row = new_row
if verbose: print(simulation_row)
return min(simulation_row[query_glass], 1.)
Optimized - Simulation only needed path¶
go
So I have a good reasonable solution, it will be better to go for a compile language, which I choosing go here. We aren’t try to be too fancy, so I’m not use go test and just setup simple test using main function before doing anything just yet
package main
func champagneTower(poured int, query_row int, query_glass int) float64 {
return 1.
}
func isEqual(a, b float64) bool {
if a < b {
return isEqual(b, a)
}
return (a - b) <= 1e-5
}
func main() {
input := []int{1, 1, 1, 2, 1, 1, 100000009, 33, 17, 25, 6, 1}
output := []float64{0.00000, 0.50000, 1.00000, 0.18750}
idx := -1
for i := 0; i < len(input); i += 3 {
idx += 1
res := champagneTower(input[i], input[i+1], input[i+2])
println("test", idx, "is", isEqual(res, output[idx]))
}
}
We seeing that, a glass can only affected (or poured) by specific amount of top glass, this mean we can calculating only on those glass to have the final answer.
- A simple recursion could work, if we don’t want to spending too much time on math to calculating exactly what we want.
- I have a map data structure
cacheto store all calculated value, that have a query(query_row, query_glass)as the map index.
Final implementation
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 09/25/2023 07:40 | Accepted | 6 ms | 7.2 MB | golang |
type Pair struct {
row int
index int
}
// Leetcode go not have min and max function built-in, so we have to implement this
func max(a float64, b float64) float64 {
if a > b {
return a
} else {
return b
}
}
func min(a float64, b float64) float64 {
if a > b {
return b
} else {
return a
}
}
func NewPair(row int, index int) Pair {
return Pair{row, index}
}
func recusion_champagneTower(poured int, query_row int, query_glass int, cache map[Pair]float64) float64 {
// println(poured, query_row, query_glass)
pair := NewPair(query_row, query_glass)
val, ok := cache[pair]
if ok {
return val
}
if poured == 0 {
return 0.
} else if query_row == 0 {
return float64(poured)
}
res := 0.
if query_glass > 0 {
res += max(recusion_champagneTower(poured, query_row-1, query_glass-1, cache)-1, 0.) / 2
}
if query_glass < query_row {
res += max(recusion_champagneTower(poured, query_row-1, query_glass, cache)-1, 0.) / 2
}
cache[pair] = res
return res
}
func champagneTower(poured int, query_row int, query_glass int) float64 {
cache := make(map[Pair]float64)
res := recusion_champagneTower(poured, query_row, query_glass, cache)
return min(res, 1.)
}
func isEqual(a, b float64) bool {
if a < b {
return isEqual(b, a)
}
return (a - b) <= 1e-5
}
Created : September 25, 2023