Problem¶
There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].
A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).
Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.
Constraints:
n == graph.length1 <= n <= 10**40 <= graph[i].length <= n0 <= graph[i][j] <= n - 1graph[i]is sorted in a strictly increasing order.- The graph may contain self-loops.
- The number of edges in the graph will be in the range
[1, 4 * 10**4].
Example 1:
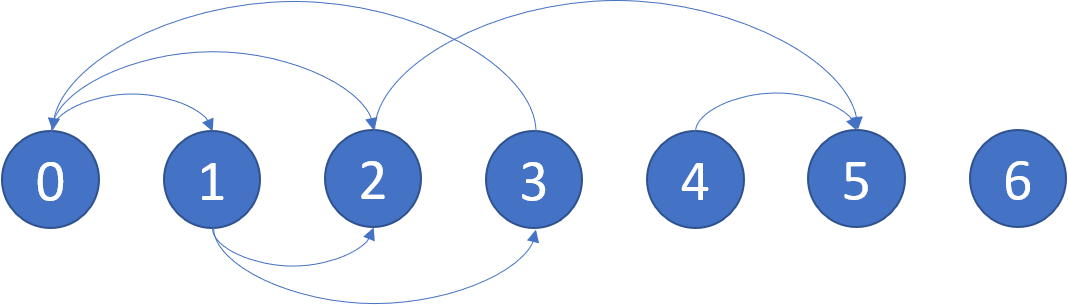
**Input:** graph = [[1,2],[2,3],[5],[0],[5],[],[|1,2],[2,3],[5],[0],[5],[],[]]
**Output:** [2,4,5,6]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
Solve¶
A hard to understand problem.
- You have terminated node, which have no outgoing edges . A terminated node is also a safe node :
if len(graph[i]) == 0 then i is "terminated node" and i is "safe node" - A safe node is node that run into a terminated node or other safe node
First approach¶
A quick O(n**3) which could be close to O(n**2) which utilize hash map do exactly that
- Find all terminated node on first loop, put it into
safe_nodearray - Find all node that only point to
safe_nodearray, which we callfound_safe_node, putting them into result - Repeat until there is no longer node to put in to
safe_nodearray - Return
safe_nodearray
class Solution: def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]: graph = [set(i) for i in graph] safe_node = set() for loop_round in range(len(graph)): found_safe_node = set() for node_id, adjNodes in enumerate(graph): if node_id in safe_node: continue if len(adjNodes) == 0: found_safe_node.add(node_id) safe_node.add(node_id) if len(found_safe_node) == 0: break for adjNodes in graph: adjNodes -= found_safe_node safe_node = list(safe_node) safe_node.sort() return safe_node
Second approach¶
Further optimize, a more better approach, where after found a safe node, we recheck other node pointed to them only.
- From input graph, create a
ref_table. Whereref_table[i]storing all node that could point/go toi - Still slow as we use too much hash map and memory though
class Solution: def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]: graph = [set(i) for i in graph] safe_node = set() ref_table = [set() for _ in graph] found_safe_node = set() for node_id, adjNodes in enumerate(graph): if len(adjNodes) == 0: found_safe_node.add(node_id) safe_node.add(node_id) for adjNode in adjNodes: ref_table[adjNode].add(node_id) for loop_round in range(len(graph)): need_to_check_node = set() new_found_safe_node = set() for node_id in found_safe_node: need_to_check_node = need_to_check_node.union(ref_table[node_id]) for node_id in need_to_check_node: graph[node_id] = graph[node_id] - found_safe_node if len(graph[node_id]) == 0: new_found_safe_node.add(node_id) safe_node.add(node_id) if len(new_found_safe_node) == 0: break found_safe_node = new_found_safe_node safe_node = list(safe_node) safe_node.sort() return safe_node
Third approach¶
We will try to minimize the need of memory allocation
- Stop try to solved and find safe node on each round of loop. Instead, checking each found safe node one by one. With simple queue/stack
found_safe_node, we check eachcurr_safe_node_idand reducing a lot of logic in our inner loop (the code implementation using simple namenode_id, changing the inner for loop interrater variable toref_node)- We can skip our need to use
set()inref_tablefor as we no longer needset.unionfunction to findneed_to_check_node(sinceneed_to_check_node = ref_table[curr_safe_node_id]) new_found_safe_nodecan be append directly intofound_safe_nodeand will be process later- On each loop, we do the same
graph[node_id] = graph[node_id] - set([curr_safe_node_id])and check if ourlen(graph[node_id]) == 0to find if it a new found safe node - The loop round can be change to a proper
while loopthat run until allfound_safe_nodeis processed
- We can skip our need to use
- Another optimization is our
safe_noderesult array, we can use a Boolean array to keep track which node is safe node instead of using set, and later loop through for anO(n)time tracking and sorting solution
class Solution: def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]: graph = [set(i) for i in graph] is_safe_node = [False] * len(graph) ref_table = [[] for _ in graph] found_safe_node = [] for node_id, adjNodes in enumerate(graph): if len(adjNodes) == 0: found_safe_node.append(node_id) is_safe_node[node_id] = True for adjNode in adjNodes: ref_table[adjNode].append(node_id) while len(found_safe_node) > 0: node_id = found_safe_node.pop(0) for ref_node in ref_table[node_id]: if is_safe_node[ref_node]: continue graph[ref_node] = graph[ref_node] - set([node_id]) if len(graph[ref_node]) == 0: found_safe_node.append(ref_node) is_safe_node[ref_node] = True safe_node = [] for node_id, is_safe in enumerate(is_safe_node): if is_safe: safe_node.append(node_id) return safe_node
Fun fact:¶
With out using
ref_nodethat we have at our second attempt, we will getTime limit Exceeded. Which mean the crafted input is quite generous on us and not have many edges case with lager input.This also mean, I not even have to optimize using set
ref_node, where every update will remove the found safe node to makeref_table[node_id]loop even lower
Here is implement we we not using ref_node
class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
graph = [set(i) for i in graph]
is_safe_node = [False] * len(graph)
found_safe_node = []
for node_id, adjNodes in enumerate(graph):
if len(adjNodes) == 0:
found_safe_node.append(node_id)
is_safe_node[node_id] = True
while len(found_safe_node) > 0:
found_safe_node_id = found_safe_node.pop()
for node_id, adjNodes in enumerate(graph):
if is_safe_node[node_id]:
continue
adjNodes -= set([found_safe_node_id])
if len(adjNodes) == 0:
found_safe_node.append(node_id)
is_safe_node[node_id] = True
safe_node = []
for node_id, is_safe in enumerate(is_safe_node):
if is_safe:
safe_node.append(node_id)
return safe_node
Read the solution and realization¶
We can still further optimization
We treat graph as literal hash map set() and tracking all node with no edge go out from it to find safe node. This could be improved by only keep track off total node can go to our current node_id instead, we call it indegree of node, where indegree[node_id] = len(graph[node_id]).
- Every terminated node and safe node only need to be visited once and we delete/reduction all edges related to that node
- This happened one time only and not overlap, so we could just keep track off total node can go to our current
node_idinstead, we call itindegreearray whereindegree[i] = len(graph[i]). - Every update,
graph[node_id] = graph[node_id] - found_safe_nodecan be replacing withindegree[node_id] -= len(found_safe_node) - We can even further simplify this process by calculating one
found_safe_nodeeach looped time, andindegree[node_id] -= 1with each loop
While I’m at it, I try to minimize the loop on ref_table too anyway
class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
indegree = [0] * len(graph)
is_safe_node = [False] * len(graph)
ref_table = [set() for _ in graph]
found_safe_node = []
for node_id, adjNodes in enumerate(graph):
if len(adjNodes) == 0:
found_safe_node.append(node_id)
is_safe_node[node_id] = True
indegree[node_id] = len(adjNodes)
for adjNode in adjNodes:
ref_table[adjNode].add(node_id)
while len(found_safe_node) > 0:
node_id = found_safe_node.pop(0)
for ref_node in ref_table[node_id]:
if is_safe_node[ref_node]:
ref_table[ref_node] -= set([node_id])
continue
indegree[ref_node] -= 1
if indegree[ref_node] == 0:
found_safe_node.append(ref_node)
is_safe_node[ref_node] = True
safe_node = []
for node_id, is_safe in enumerate(is_safe_node):
if is_safe:
safe_node.append(node_id)
return safe_node
^Simulation
Just getting it¶
Here is some of the best Crtl + C solution
- We create a mark array for caching result of
Helperfunction- It start at
-1for not doing any calculation yet
- It start at
Helpercheck if a node issafeor not:- Where with each
node, we actually try to do a DFSHelperfunction and find if our DFS search function through graph ran in to a visitednode. - The function keep track of visited node by marking them as
0 - If any of
HelperDFS search that haveadjNodeconnected to our current nodeidxingraph[idx]return0(Which mean it have been visited by theHelperDFS function or run into a know not safe node), return0which mean our current nodeidxis not safe - Otherwise, our current node
idxis a safe node, cache the result into ourmarkcache array and return1
- Where with each
I try to be more clear changing all function and variable name, but this have some quite elegant, and quite challenging to break it down into smaller component:
- Keeping track of visited node into
is_safe_nodearray by using 3 stage[None, False, True] - Pre-set our current node
current_node_idinto unsafe node (is_safe_node[current_node_id] = falsestage phase) until proven a safe node (is_safe_node[current_node_id] = Truestage). Each connection/edge of ourcurrent_node_id -> adj_node_idwill be check to see if:- when we have a
adj_node_idwith aFalsenode stage:adj_node_ideither is a Visited node in current call stack BFS path that and currently being Pre-set as unsafe node (which mean it haven’t been proven a safe node). This mean our BFS function found a cycle path (or can’t be terminated path) from our current call stack BFS path.- or
adj_node_idis an already know unsafe node that have been process. We can start a cycle path from thisadj_node_idnode
- We have a
adj_node_idwithTruenode stage:- Which mean it pass it the pre-set phase, no cycle path can be from start from this
adj_node_idnode - And
adj_node_idbecome a know safe node that have been process
- Which mean it pass it the pre-set phase, no cycle path can be from start from this
- when we have a
- Immediately return a
DFSasFalsewill break out of all our current call stack, which make all node trace down preset as unsafe node is now become a know a unsafe node.
class Solution:
def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
is_safe_node = [None] * len(graph)
def DFS(current_node_id):
if not is_safe_node[current_node_id] is None:
return is_safe_node[current_node_id]
is_safe_node[current_node_id] = False
for adj_node_id in graph[current_node_id]:
if DFS(adj_node_id) == False:
return False
is_safe_node[current_node_id] = True
return True
return [node_id for node_id in range(len(graph)) if DFS(node_id)]
^DFS
Comparation¶
Overall, a too intelligent DFS code for sure, that reduce about ~100 ms ~ 1/7 time complexity (Here is comparation of DFS (Bellow row) and Simulation (Above row) code implementation)
| Agro | Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|---|
| Simulation | 07/13/2023 11:05 | Accepted | 716 ms | 25 MB | python3 |
| DFS | 07/13/2023 11:04 | Accepted | 634 ms | 24.2 MB | python3 |
Created : August 16, 2023