Skip to content

847. Shortest Path Visiting All Nodes

Problem

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

Pasted image 20230917104410.png

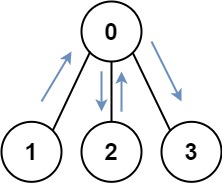
Input: graph = [[1,2,3],[0],[0],[0|1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

Pasted image 20230917104400.png

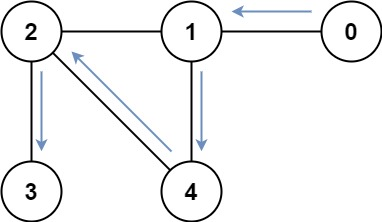
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2|1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Constraints:

  • n == graph.length
  • 1 <= n <= 12
  • 0 <= graph[i].length < n
  • graph[i] does not contain i.
  • If graph[a] contains b, then graph[b] contains a.
  • The input graph is always connected.

Solve

White board

My white board be like

Pasted image 20230917104342.png
Pasted image 20230917104437.png

Need to work more before start coding

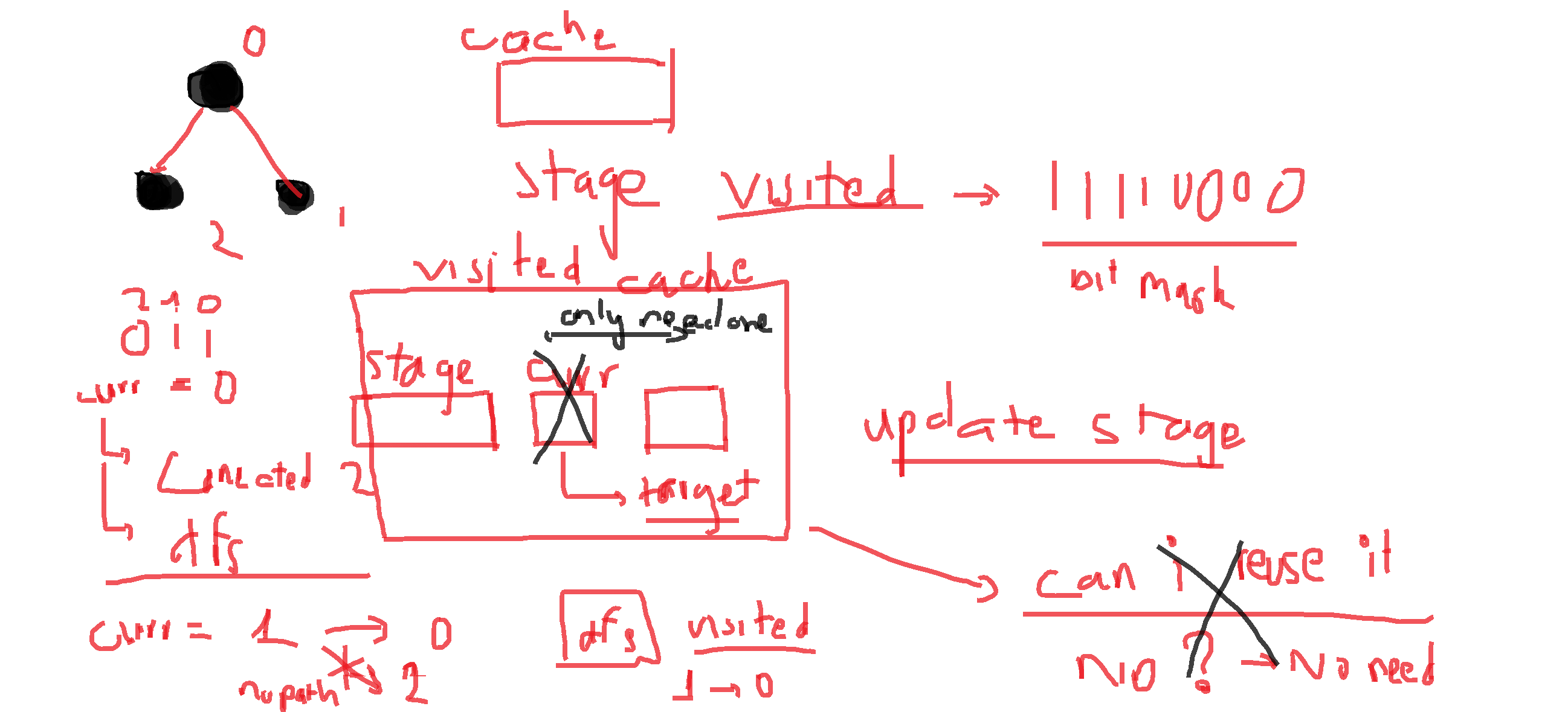
  • Frist I try to use a cache, to find anything that we can store into memory, that needed to solve the problem
    • I quickly thought about storing the stage of current problem, we are given:
      • Current curr start point (I assuming it need to be node 0 for started node, the problem said we can chose any for start node, RTFM moments)
      • A list of Node in graph that need to be visited
    • For the purpose
      • I try saving a target next point that we are try to go to next
      • This is base on that, a stage can be un-change, we need to go to the next point so that we can go to the next point (huh?) that can update the stage.
      • Example, when we start at [0] -> [1], we need to go back to [0] before getting back to [2] (result path [0] -> [1] -> [0] -> [2])
        Pasted image 20230917105257.png
      • This make me think that I want to save the stage of this kind of updated interaction (so I not repeating it again)
      • So, we have 3 parameters, cache contain the value of the total step that get to that stage:
        stage = [0], start = 0, target = 1 -> step = 1
        stage = [0, 1], start = 1, target = 0 -> step = 2
        stage = [0, 1], start = 0, target = 2 -> step = 3
    • This is good enough:
      • A cache that storing all possible finite update
      • The value that cache store being update every step that telling us how much step needed to reach that stage
      • We can stop the updating if stage contain all the node
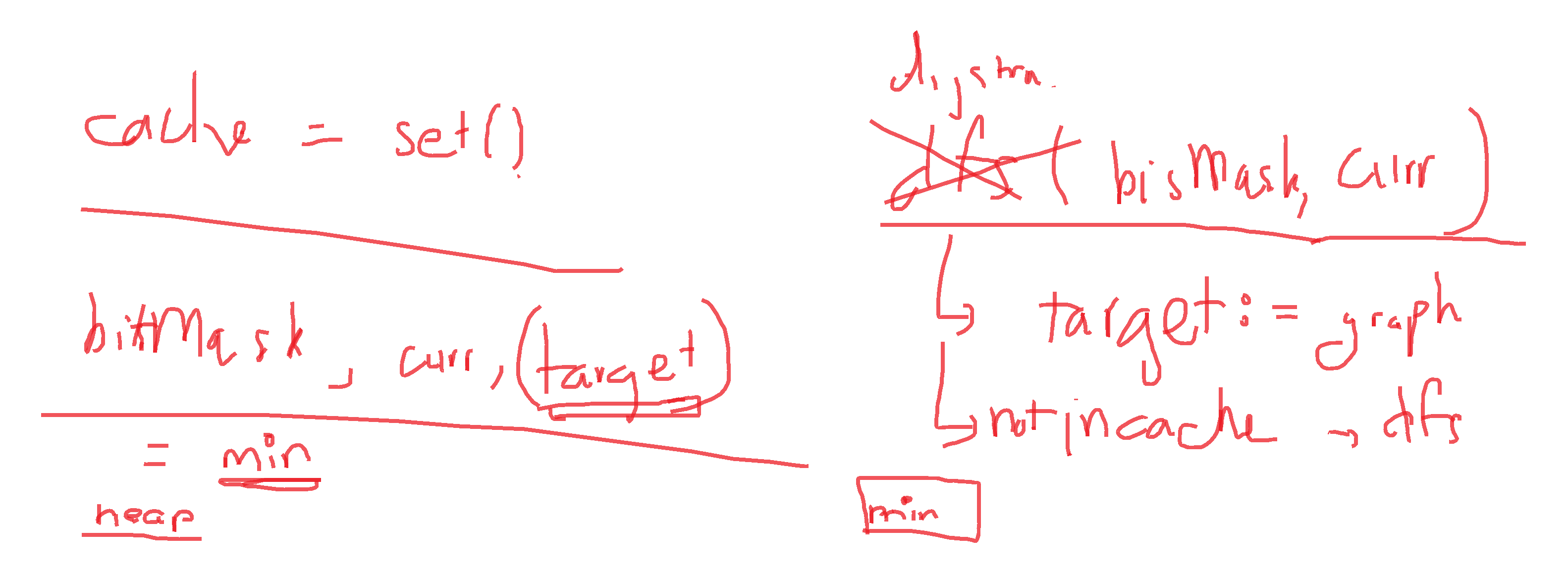
  • By roughly though of the Algorithm, I think of this:
    • A Dijkstra -like:
      • Chose the lowest step in cache
      • Update all possible next stage it can reach to
      • This require us to keep trach an not repeat processing old stage
    • Data structure - Heap:
      • So we can easily find the min value in O(1)

Dijkstra + Heap, cache on every update

dynamic_programing

First implement - Separated start node run

My first implement

  • I try every started node in a separated run
  • This result into a nested n loop, updating a possible cache size of (n ** 2 * 2 ** n). Making it a worst possible O(n ** 3 * 2 ** n) time complexity (n just too small so I just skip log n time to push and pop heap, maybe it wrong though)
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        MAXSTAGE = (1<<(n))-1

        def tryStartAt(index):
            cache = [[[-1] * n for i in range(n)] for _ in range(MAXSTAGE+1)]
            shortest = -1

            heap = []

            def setbit(mask, pos):
                return mask | (1 << (pos))

            heap.append((0,(setbit(0, index),index)))

            while len(heap) > 0: 
                acumulated, (stage, start) = heappop(heap)
                if stage == MAXSTAGE:
                    shortest = acumulated
                    break
                for target in graph[start]:
                    if cache[setbit(stage, target)][start][target] == -1: 
                        nextStage = setbit(stage, target)
                        cache[nextStage][start][target] = acumulated + 1
                        heappush(heap, (acumulated + 1, (nextStage, target)))
            return shortest

        minimum = -1
        for i in range(n):
            curr = tryStartAt(i)
            if minimum == -1 or minimum > curr:
                minimum = curr
        return minimum

Optimizing 1 - All node at started

O(n ** 2 * 2 ** n)

Instead of using a separated run, we can adding all started node directly into the cache, this mean we can use any other started stage to optimize the cache matrix

  • This thus reduce the nested loop, we only need to update cache table with possible size n ** 2 * 2 ** n
  • Worst case will be O(n ** 2 * 2 ** n) (again, I skip log n time using on heap push, pop as n is very small)
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        MAXSTAGE = (1<<(n))-1

        cache = [[[-1] * n for i in range(n)] for _ in range(MAXSTAGE+1)]
        shortest = -1

        heap = []

        def setbit(mask, pos):
            return mask | (1 << (pos))

        for index in range(n):
            heap.append((0,(setbit(0, index),index)))

        while len(heap) > 0: 
            acumulated, (stage, start) = heappop(heap)
            if stage == MAXSTAGE:
                shortest = acumulated
                break
            for target in graph[start]:
                if cache[setbit(stage, target)][start][target] == -1: 
                    nextStage = setbit(stage, target)
                    cache[nextStage][start][target] = acumulated + 1
                    heappush(heap, (acumulated + 1, (nextStage, target)))

        return shortest

Optimizing 2 - Less cache stage

O(n * 2 ** n)

A Visited Stage, start -> target stage making us repeat processing to get to a same (Visited Stage, Current node).

We not need to save start node in cache at all, this is because that we always have the minimum possible step using heap, making every update is the best possible total path step to reach (Visited Stage, Current node).

This mean we can drop [start] from cache, reducing possible cache size to n * 2 ** n. Reduce possible worst time complexity to O(n * 2 ** n) (again, I skip log n time using on heap push, pop)

class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        MAXSTAGE = (1<<(n))-1

        visited = set()
        shortest = -1

        queue = deque()

        def setbit(mask, pos):
            return mask | (1 << (pos))

        for index in range(n):
            queue.append((0,(setbit(0, index),index)))

        while len(queue) > 0: 
            acumulated, (stage, start) = queue.popleft()
            if stage == MAXSTAGE:
                shortest = acumulated
                break
            for target in graph[start]:
                if (setbit(stage, target), target) not in visited: 
                    nextStage = setbit(stage, target)
                    visited.add((setbit(stage, target), target))
                    queue.append((acumulated + 1, (nextStage, target)))

        return shortest

Biggest realization - BFS + Queue

BFS

  • As we always have the best accumulated on every step. This make heap isn’t necessary, and can be transfer into a First in, First out Queue data structure
  • Also, the Dijkstra not necessary to contain the accumulated, every visited have the best possible value (a BFS traversal on possible stage graph)

Now this, make it a true O(n * 2 ** n) solution

class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)
        MAXSTAGE = (1<<(n))-1

        visited = set()
        shortest = -1

        queue = deque()

        def setbit(mask, pos):
            return mask | (1 << (pos))

        for index in range(n):
            queue.append((0,(setbit(0, index),index)))

        while len(queue) > 0: 
            acumulated, (stage, start) = queue.popleft()
            if stage == MAXSTAGE:
                shortest = acumulated
                break
            for target in graph[start]:
                if (setbit(stage, target), target) not in visited: 
                    nextStage = setbit(stage, target)
                    visited.add((setbit(stage, target), target))
                    queue.append((acumulated + 1, (nextStage, target)))

        return shortest
Last update : September 17, 2023
Created : September 17, 2023