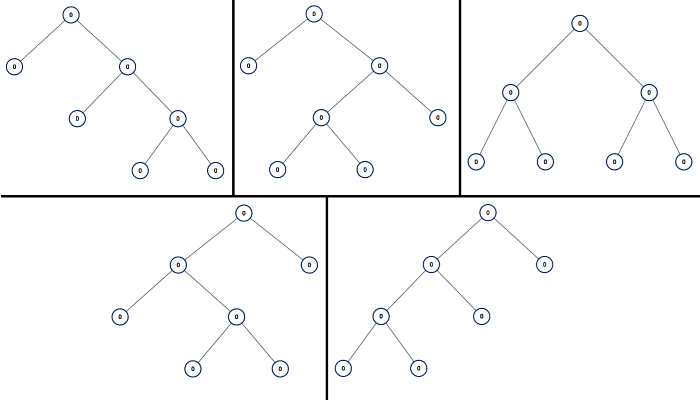
Problem¶

Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Example 1:

**Input:** n = 7
**Output:** [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0|0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Constraints:

• 1 <= n <= 20

Solve¶

Over complicating simulation approach¶

hash

There isn’t any thing said we could reused the tree node, which I mean all TreeNode object from Root A should be different from Root B . We assuming that this No reused rule is required.

We try to build up all solution from bottom:

• If n is even (n % 2 == 0), there are no possible full binary trees since we always need to have an odd number of nodes to form a full binary tree.
• If n is 1, there is only one possible full binary tree with a single node having a value of 0.

For any odd n = 2x + 1, where x is an integer, we can generate the full binary trees from the previous n - 2 = 2x - 1 trees. We use the following building blocks:

• self.roots: We keep track of an array of roots math have previous n-2 nodes, which starting with a tree containing a single node with value 0 when n = 1.
• self.leafs: We also keep track of all leaf nodes in each tree of self.roots array. The purpose of this is to quickly add new nodes directly to the leaf nodes instead of looping through all the nodes to find the leaf nodes.

In the implementation, I using tuple to store both of self.roots and self.leafs in one array self.roots

We then follow these steps to build the trees:

1. We start with n = 1, and initialize self.roots with a tree containing a single node with value 0. Also, we initialize self.leafs[root] = [<all leaf nodes of the root tree>].
2. For any n = 2x + 1 (where n = 3, 5, 7, ...), we try to generate new trees from the previous n - 2 trees. To do this efficiently:
   1. We loop through each curr_root root tree in self.roots and their corresponded self.leafs
   2. (Step 2) Add two leaf nodes to any of this root leaf.
   3. Use the copyTree function to create a copy of the all tree and then revert the change from step 2.
   4. We then hash the new tree using the hashNode function to check for any collision with previously generated trees.
   5. If there is no collision (the hash is not in visited), we add the new tree to the result list along with its leaf nodes.
   6. Update our self.roots to new result
3. We continue this process until we reach n. Finally, we return the generated trees in self.roots

The simulation-based approach works, but it is unnecessarily complex and slow due to the copying of trees and hash computations.

class Solution:
    def hashNode(self, root, index = 1):
        if root is None:
            return 0
        result = index << 5 + index
        if root.left:
            result += self.hashNode(root.left, 2*index)
        if root.right:
            result += self.hashNode(root.right, 2*index + 1)
        return result

    def copyTree(self, source):
        result = None
        leafs = []
        result = TreeNode(source.val)
        if source.left:
            result.left, leafsLeft = self.copyTree(source.left)
            leafs += leafsLeft
        if source.right:
            result.right, leafsRight = self.copyTree(source.right)
            leafs += leafsRight
        if source.left is None and source.right is None:
            leafs.append(result)
        return result, leafs

    def addLeaf(self):
        result = []
        visited = set()
        for root, leafs in self.roots:
            for leaf in leafs[::-1]:
                leaf.left = TreeNode(0)
                leaf.right = TreeNode(0)

                new_root, new_leafs = self.copyTree(root)
                hashN = self.hashNode(new_root)
                if hashN not in visited:
                    result.append((new_root, new_leafs))
                    visited.add(hashN)

                leaf.left = None
                leaf.right = None
        return result

    def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:
        if n%2 == 0:
            return []
        self.roots = []
        for i in range(1, n+1, 2):
            tmp = []
            if i == 1:
                root = TreeNode(0)
                tmp = [(root, [root])]
                self.roots = tmp
                continue
            tmp = self.addLeaf()
            self.roots = tmp

        return [root for root, _ in self.roots]

Minimal¶

The simulation approach can be greatly simplified using dynamic programming and memorization to avoid redundant computations.

We use the following steps to find all possible full binary trees with n nodes:

1. If n is even (n % 2 == 0), there are no possible full binary trees, so we return an empty list.
2. If n is 1, there is only one possible full binary tree with a single node having a value of 0. We return this tree as a list containing a single node.
3. For any odd n = 2x + 1 (where x is an integer), we recursively find all possible full binary trees for each possible left subtree with nodes i (where i ranges from 1 to n - 1 with a step of 2), and the right subtree with nodes n - i - 1. We then combine these left and right subtrees with a root having a value of 0, and add them to the result list.
4. We use memorization to store the results of subproblems in the cache dictionary to avoid redundant computations.

The minimal approach is much more efficient and straightforward, and it accurately finds all possible full binary trees with n nodes, each having a root node with a value of 0. It returns the final list of trees in any order.

class Solution:
    def allPossibleFBT(self, n: int, cache = None) -> List[TreeNode]:
        if cache is None:
            cache = {}

        if n in cache:
            return cache[n]

        if n % 2 == 0:
            return []
        if n == 1:
            cache[n] = [TreeNode()]
            return [TreeNode()]

        res = []
        for i in range(1, n, 2):
            left = self.allPossibleFBT(i, cache)
            right = self.allPossibleFBT(n - i - 1, cache)

            for l in left:
                for r in right:
                    root = TreeNode(0, l, r)
                    res.append(root)

        cache[n] = res
        return res