1326. Minimum Number of Taps to Open to Water a Garden

Problem¶

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

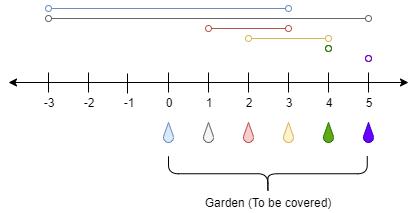
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Constraints:

1 <= n <= 10 ** 4
ranges.length == n + 1
0 <= ranges[i] <= 100

Solve¶

1326. White Board - Minimum Number of Taps to Open to Water a Garden file not exists

We can greedy choosing the best possible tap every step (which covered the most range possible)
This can be done quickly by sorting the range being covered
We start from the lowest start of range, as it sorted, we can’t going back to covered that range any more, so every time, we want to chose the best of the current start range
- If we can’t find any, we can return -1 , as we need the range to be fully covered
- If we can find any:
  - Adding it to possible queue q
  - Keep running until start of range go our of scope.
  - Get the max end of range in our q.
Update the current end as our new start point.

Sorted - preprocessing data - chose the best one.¶

O(n log n)

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        covered = [ (max(0, pos - rang) , pos + rang) for pos, rang in enumerate(ranges)]

        def sortKey(x):
            return -x[1]

        covered.sort(key = sortKey)


        def sortKey(x):
            return x[0]

        covered.sort(key = sortKey)

        curr = None
        total = 0
        q = []
        for i, j in covered:
            if curr is None:
                curr = j
                total += 1
                continue
            if curr < j and curr >= i:
                q.append(j)
                continue
            if len(q) == 0:
                return -1
            curr = max(q)
            total += 1
            q = []
        if len(q) > 0:
            total += 1
        return total

Problem:¶

Coverage range
- What I skip (from the problem) is that: The water coverage of each tap is on the tile, while the position of the tap, is the middle, which mean 0 will not covering anything (While 1 will cover 2 tiles).
- Still, as I representing covered range as (max(0, pos - rang) , pos + rang), we can just not including pos + rang in the ranges, this will work wonder
Not handle the finishing range well:
- Only n is needed, which mean, if the covered range is curr > n, we can return the total, instead of keep looping.
- This can also be fixed if we create a max cap for covered range, by adding min(pos + rang, n) instead of just pos + rang
Adding the current tap to queue, right after choosing tap. As I only use q = [], the current tap isn’t being processed. q.append(j)
Adding more skip:
- If covered range curr is already covered the current tap, curr >= j , we can skip over the tap, this also make the choosing next tap curr = max(q) less bug
- This also mean adding condition the current tap if (curr < j): q.append(j) from (3)

Final implementation¶

Time Submitted	Status	Runtime	Memory	Language
08/31/2023 10:02	Accepted	117 ms	18.2 MB	python3

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        covered = [ (max(0, pos - rang) , min(pos + rang, n)) for pos, rang in enumerate(ranges)]
        # print(covered)

        def sortKey(x):
            return -x[1]

        covered.sort(key = sortKey)


        def sortKey(x):
            return x[0]

        covered.sort(key = sortKey)
        # print(covered)
        curr = None
        total = 0
        q = []
        for i, j in covered:
            # print(curr, i, j, q)
            if curr is None:
                curr = j
                total += 1
                continue
            if curr >= j:
                continue
            if curr < j and curr >= i:
                q.append(j)
                continue
            if len(q) == 0:
                return -1
            curr = max(q)
            total += 1
            q = []
            if (curr < j):
                q.append(j)
        if len(q) > 0:
            total += 1
        return total

Time complexity: O(n log n)

Sorted covered range, make it O(n log n)
There is 2 loop, first loop is O(n)
The second, is max(q) is independent with the first loop, cost O(n)

We can reduce the need to call max(q), to reducing even more space needed. But this also mean we want a better way to store covered, which already cost O(n) space.

Optimizing - No more sort¶

O(n)

I used the same input processing as the Solve that Leetcode done, this way, I can reduce the need of sorting the covered range.

Time Submitted	Status	Runtime	Memory	Language
08/31/2023 12:16	Accepted	121 ms	17 MB	python3

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        covered = [-1] * (n + 1)

        for i, r in enumerate(ranges):
            covered[max(0, i - r)] = min(n, i + r)

        curr = None
        total = 0
        q = []
        for i, j in enumerate(covered):
            # print(curr, i, j, q)
            if curr is None:
                curr = j
                total += 1
                continue
            if curr >= j:
                continue
            if curr < j and curr >= i:
                q.append(j)
                continue
            if len(q) == 0:
                return -1
            curr = max(q)
            total += 1
            q = []
            if (curr < j):
                q.append(j)
        if len(q) > 0:
            total += 1
        return total

Optimizing 2 - No more `Max(arr)`¶

O(n)

It still a nested loop (even it independent with above loop) with a lot of memory allocating for array vector q.
This could be done over a single nextMax variable.

Time Submitted	Status	Runtime	Memory	Language
08/31/2023 12:20	Accepted	119 ms	16.8 MB	python3

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        covered = [-1] * (n + 1)

        for i, r in enumerate(ranges):
            covered[max(0, i - r)] = min(n, i + r)

        curr = None
        total = 0
        nextMax = -1
        for i, j in enumerate(covered):
            if curr is None:
                curr = j
                total += 1
                continue
            if curr >= j:
                continue
            if curr < j and curr >= i:
                nextMax = max(nextMax, j)
                continue
            if nextMax == -1:
                return -1
            curr = nextMax
            total += 1
            nextMax = -1
            if (curr < j):
                nextMax = max(nextMax, j)
        if nextMax > 0:
            total += 1
        return total

Actual O(n)¶

O(n)

The cleaver way to preprocess the data

        # Create a list to track the maximum reach for each position
        max_reach = [0] * (n + 1)

        # Calculate the maximum reach for each tap
        for i in range(len(ranges)):
            # Calculate the leftmost position the tap can reach
            start = max(0, i - ranges[i])
            # Calculate the rightmost position the tap can reach
            end = min(n, i + ranges[i])

            # Update the maximum reach for the leftmost position
            max_reach[start] = max(max_reach[start], end)

This way we can effective create the same data which our sort want to achieved.

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        # Create a list to track the maximum reach for each position
        max_reach = [0] * (n + 1)

        # Calculate the maximum reach for each tap
        for i in range(len(ranges)):
            # Calculate the leftmost position the tap can reach
            start = max(0, i - ranges[i])
            # Calculate the rightmost position the tap can reach
            end = min(n, i + ranges[i])

            # Update the maximum reach for the leftmost position
            max_reach[start] = max(max_reach[start], end)

        # Number of taps used
        taps = 0
        # Current rightmost position reached
        curr_end = 0
        # Next rightmost position that can be reached
        next_end = 0

        # Iterate through the garden
        for i in range(n + 1):
            if i > next_end:
                # Current position cannot be reached
                return -1

            if i > curr_end:
                # Increment taps when moving to a new tap
                taps += 1
                # Move to the rightmost position that can be reached
                curr_end = next_end

            # Update the next rightmost position that can be reached
            next_end = max(next_end, max_reach[i])

        # Return the minimum number of taps used
        return taps

Last update : September 17, 2023
Created : September 3, 2023

1326. Minimum Number of Taps to Open to Water a Garden

Problem¶

Solve¶

Sorted - preprocessing data - chose the best one.¶

Problem:¶

Final implementation¶

Optimizing - No more sort¶

Optimizing 2 - No more Max(arr)¶

Actual O(n)¶

Optimizing 2 - No more `Max(arr)`¶