1615. Maximal Network Rank
Problem¶
There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.
The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.
The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.
Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.
Example 1:
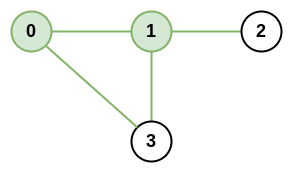
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3|0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
Example 2:
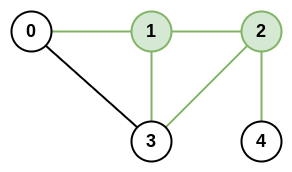
Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4|0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.
Example 3:
Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7|0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
Constraints:
2 <= n <= 1000 <= roads.length <= n * (n - 1) / 2roads[i].length == 20 <= a_i, b_i <= n-1a_i != b_i- Each pair of cities has at most one road connecting them.
Solve¶
Preprocess data¶
python
Consider this <city, road> problem as a graph <node, edge>
Before hand, we can calculating each node rank. Which define as the total number of out going edge of the node:
The roads array is a graph represent in edges array:
- Which each connection in graph, we call it a edge
(u,v) - All connection
(u,v)of graph is contain inE = roadsarray
which not that great for most of graph problem. We process it to have a adjacent table adjNode instead:
- Each node
xin graph have all adjacent node inadjNode[i]array - All connection of graph then is contain in
adjNodetable
This mean, by creating adjNode from road, we also can get the rank of node x by taking the length of correspond adjNode[x]
class Solution:
def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
adjNode = [[] for i in range(n)]
nodeRank = []
for (u,v) in roads:
adjNode[v].append(u)
adjNode[u].append(v)
for i in range(n):
nodeRank.append(len(adjNode[i]))
print(nodeRank)
Brute force / Try all possible¶
python
By talking all the possible combination of 2 node, we can easily calculating the maximum rank needed to be return.
The problem specific this:
If a road is directly connected to both cities, it is only counted once.
So, to calculating a combination rank of 2 node i and j, we need to consider:
- If there is a
(i,j)edge (we can check it usingi in adjNode[j]), it already innodeRank[i] + nodeRank[j]sum, and need to be reduce by one. - Other wise this isn’t needed and
nodeRank[i] + nodeRank[j]sum being keep the same
This is function, the trick is that Boolean numeric value is True = 1 and False = 0, we can handle the if logic by using this trick in python using an int type cast.
This mean:
- int(i in adjNode[j]) = -int(True) = -1- int(i in adjNode[j]) = -int(False) = -0
Final implementation:
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/18/2023 22:03 | Accepted | 291 ms | 18.1 MB | python3 |
class Solution:
def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
adjNode = [[] for i in range(n)]
nodeRank = []
for (u,v) in roads:
adjNode[v].append(u)
adjNode[u].append(v)
for i in range(n):
nodeRank.append(len(adjNode[i]))
maximal = 0
for i in range(n):
for j in range(i+1, n):
possible = nodeRank[i] + nodeRank[j] - int(i in adjNode[j])
if maximal < possible:
maximal = possible
return maximal
Connected table/matrix with brute force¶
python
Instead of adjacent table, we could also use Connected table matrix, as with:
- With edge
(u,v)is in graph, we representing them in amatrix[u,v] = True - With edge
(u,v)isn’t in graph, we representing them in amatrix[u,v] = False
This is way nice than previous one, costing O(1) to check if the (u,v) edge is in the graph or not, where we using (i in array) expression, which need to loop through all element in the worst case scenario.
While we can use hash map, but it cost a lot more time to allocating that much memory, especially in python.
As we have 2 <= n <= 100 , which mean n is small enough, this Connected table matrix of representation is way more fitting.
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/18/2023 22:03 | Accepted | 291 ms | 18.1 MB | python3 |
class Solution:
def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
adjNode = [[False] * n for i in range(n)]
nodeRank = [0] * n
for (u,v) in roads:
adjNode[u][v] = True
adjNode[v][u] = True
nodeRank[u] += 1
nodeRank[v] += 1
maximal = 0
for i in range(n):
for j in range(i+1, n):
possible = nodeRank[i] + nodeRank[j] - int(adjNode[i][j])
if maximal < possible:
maximal = possible
return maximal
Edge only representation with sort, binary search and brute force¶
python
A no one ask for solution, while we reduce the need to preprocessing data. Using just edges need a lot of thing to reduce the time complexity from O(n**4) down to O(n**2 * log(n**2))
- Quickly check
(u,v)in graph - Quickly calculating all rank of individual
u
A possible thing to do is quickly sort roads array, and using binary search to check if any (u,v) in the roads array
To standardize (u, v), as it’s bi-direction, we enforce rule that u < v in all case. So we need to update all roads.
This also come with a lot of manual touch to finish like:
- Checking if roads is empty, which make our binary search throw error in runtime;
- Manually loop through all the node to update rank
- Using special sort that can handle two value comparing
(u, v)
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/18/2023 22:43 | Accepted | 478 ms | 17.8 MB | python3 |
class Solution:
def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
if len(roads) == 0:
return 0
rank = [0] * n
for i, (u, v) in enumerate(roads):
if u > v:
roads[i] = (v, u)
rank[u] += 1
rank[v] += 1
def sortKey(road):
u, v = road
return 1000*u + v
roads.sort(key = sortKey)
def search(u,v):
l = -1
r = len(roads)
while l < r:
m = (l + r) // 2
x, y = roads[m]
if l == m:
if l < 0:
return False
return (x == u) and (y == v)
elif (u < x) or (x == u and v < y):
r = m
else:
l = m
return False
maximal = 0
for i in range(n):
for j in range(i+1, n):
possible = (rank[i] + rank[j]) - int(search(i, j))
if maximal < possible:
maximal = possible
return maximal
Edge only with hash map, brute force¶
python
By using hash function, we can easily check if (u,v) in roads in O(1) time, which could be on pair with Connected table/matrix solution.
While we can directly convent roads to set() in python, we need to handle case where (u,v) is in road, but (v,u) is not.
| Time Submitted | Status | Runtime | Memory | Language |
|---|---|---|---|---|
| 08/18/2023 22:39 | Accepted | 307 ms | 18.7 MB | python3 |
class Solution:
def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
if len(roads) == 0:
return 0
cache = set()
rank = [0] * n
for u, v in roads:
rank[u] += 1
rank[v] += 1
if u > v:
cache.add((v,u))
else:
cache.add((u,v))
maximal = 0
for i in range(n):
for j in range(i+1, n):
possible = (rank[i] + rank[j]) - int((i, j) in cache)
print(possible, i, j)
if maximal < possible:
maximal = possible
return maximal
Created : August 18, 2023