1658. Minimum Operations to Reduce X to Zero

Problem¶

You are given an integer array nums and an integer x. In one operation, you can either remove the leftmost or the rightmost element from the array nums and subtract its value from x. Note that this modifies the array for future operations.

Return the minimum number of operations to reduce x to exactly 0 if it is possible__, otherwise, return -1.

Example 1:

Input: nums = [1,1,4,2,3], x = 5
Output: 2
Explanation: The optimal solution is to remove the last two elements to reduce x to zero.

Example 2:

Input: nums = [5,6,7,8,9], x = 4
Output: -1

Example 3:

Input: nums = [3,2,20,1,1,3], x = 10
Output: 5
Explanation: The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.

Constraints:

• 1 <= nums.length <= \(10^5\)
• 1 <= nums[i] <= \(10^4\)
• 1 <= x <= \(10^9\)

Solve¶

White board¶

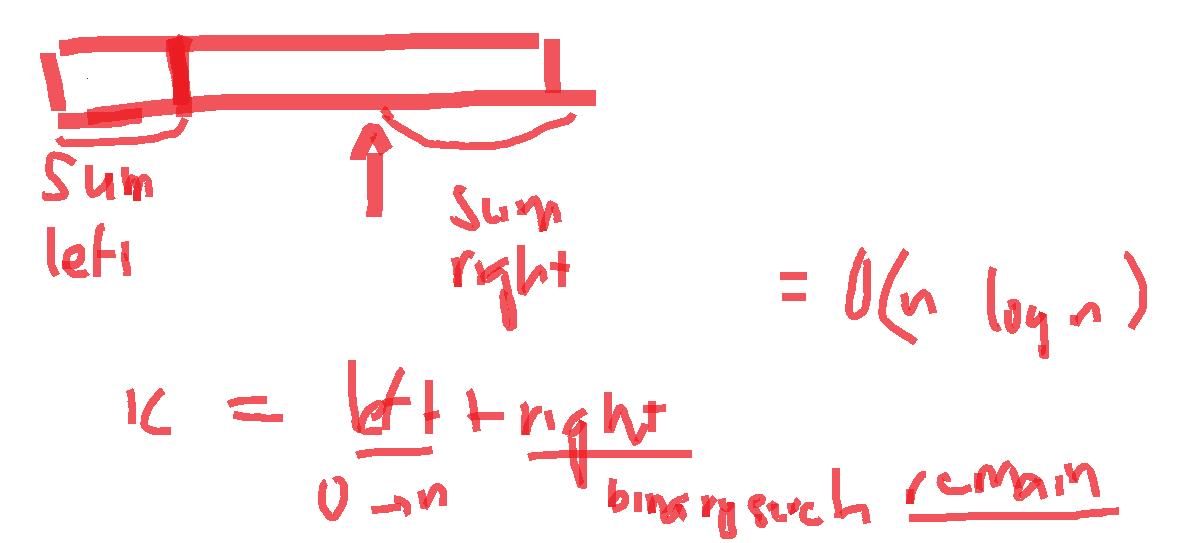
• We can describe x = sum(nums[0:left]) + sum(nums[right:n]) where (left + n-right) is minimum
• The ideal is that, there is a middle point to use binary search:
  • By trying each left (making left and sum(nums[0:left]) constant on each loop) , we have a remain sum(nums[right:n]) = x - sum[:left] to full fill
  • With right travel between [left .. n] (no overlapping). We always have
  • sum(nums[left:n]) < sum(nums[left+1:n]) < .. < sum(nums[n:n]) = 0 (as 1 <= \(nums_i\) <= \(10^4\)).
  • We need to find a sum(nums[right:n]) = x - sum[:left] inside a sorted array, making it become a binary search problem
• This mean, we need a way to easily calculating sum(nums[x:n]), which is quite easy and can be stored in a O(n) space array.

Build-in python - Binary search + Preprocessing Sum range¶

O(n log n)

I instead making right a static, and find left using binary search

• I pre-calculating all range nums[0:0], nums[0:1], … , nums[0:n] (n = len(nums)) and storing them in sumRange array.

• We have some built-in binary search, which I used here bisect_right: bisect_right return a position where sumRange[:position] <= x < sumRange[:position+1]on a sorted array, args hi = right+1 is there to force result not cause a overlapping. Using help(bisect.bisect_right) for the explanation

Final implementation is here:

class Solution:
    def minOperations(self, nums: List[int], x: int) -> int:
        n = len(nums)
        sumRange = [0] * (n + 1)

        for i in range(n):
            sumRange[i+1] = sumRange[i] + nums[i]

        def getSum(x,y):
            return sumRange[y] - sumRange[x]

        minOps = n + 1
        for right in range(n, -1, -1):
            rightSum = getSum(right, n)
            leftSum = x - rightSum
            insertPos = bisect_right(sumRange, leftSum, hi = right+1)
            # print(sumRange[insertPos-1] - leftSum, insertPos, right)
            if sumRange[insertPos-1] == leftSum:
                possible = insertPos-1 + n - right
                if minOps > possible:
                    minOps = possible
                # print(possible)
        # print(n + 1)
        if minOps != n + 1:
            return minOps
        return -1

Linear finding?¶

O(n)

We are sure that, rightSum is always increasing, which mean, leftSum always decreasing, which mean left is always decreasing.

We now instead have a sliding window like problem (but revert - sum outsize vs sum inside, not that much of a different here)

• Every right increasing, left is sliding until sum equal smaller than x
• This making we, need to increasing right.
• Record every sliding window hit where sum = x, update minimum value

Left and right loop only travel in one direction and is independent, making this a O(n) times complexity

• Still, I use a binary search for the first init value.
• In fact, If I remove all together sumRange and all in on sliding window, we could get O(1) in space, which is optimal solution I can get from this approach

Final implementation:

class Solution:
    def minOperations(self, nums: List[int], x: int) -> int:
        n = len(nums)
        sumRange = [0] * (n + 1)

        for i in range(n):
            sumRange[i+1] = sumRange[i] + nums[i]

        def getSum(x,y):
            return sumRange[y] - sumRange[x]

        minOps = n + 1
        insertPos = -1
        for right in range(n, -1, -1):
            rightSum = getSum(right, n)
            leftSum = x - rightSum
            if insertPos == -1:
                insertPos = bisect_right(sumRange, leftSum, hi = right+1)
            else:
                while insertPos > 0:
                    if sumRange[insertPos-1] <= leftSum:
                        break
                    insertPos -= 1
            # print(sumRange[insertPos-1] - leftSum, insertPos, right)
            if sumRange[insertPos-1] == leftSum:
                possible = insertPos-1 + n - right
                if minOps > possible:
                    minOps = possible
                # print(possible)
        # print(n + 1)
        if minOps != n + 1:
            return minOps
        return -1