Problem¶
You are given an array of events where events[i] = [startDay_i, endDay_i, value_i]. The ith event starts at startDay_i and ends at endDay_i, and if you attend this event, you will receive a value of value_i. You are also given an integer k which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return the maximum sum of values that you can receive by attending events.
Constraints:
1 <= k <= events.length1 <= k * events.length <= 10**61 <= startDay_i <= endDay_i <= 10**91 <= valuei <= 10**6
Example 1:
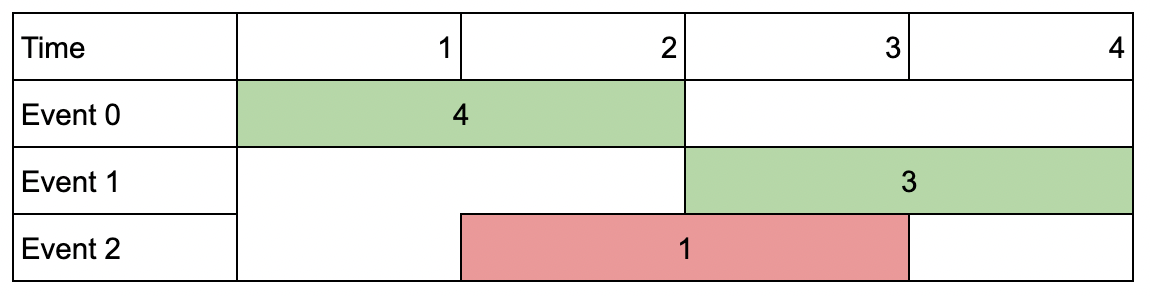
**Input:** events = [[1,2,4],[3,4,3],[2,3,1|1,2,4],[3,4,3],[2,3,1]], k = 2
**Output:** 7
**Explanation:** Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
Solve¶
My first thought is some dynamic programing that we try to get all possible events instead of having to limit our self with only visit k event. Storing them in a lookup array, I could found a pattern:
- Go from first event to the last event that sorted by
endvalue - Try to calculating the best total value we can get with each the
endvalue. Because we have a quite large range ofendDay_i in [1..10**9]. So I implement a Binary search and reduce the need to storing[1..10**9]possibleendvalue.- As the end day is inclusive, so we need to find index where
key[index-1] < start <= key[index]. Wherekey = events_end[0..current_event_index]
- As the end day is inclusive, so we need to find index where
- When calculate the best possible total value of event with each
lookup[end]. we have either:- (Case 1) Last found best event
lookup[end] = lookup[end-1] - (Case 2) Choosing current event and best found
lookup[end_before]withend_before < start[index]or we can saidlookup[end] = value_of_current_event + lookup[start-1]
- (Case 1) Last found best event
end-1orstart-1here is just for representation, as I try to minimize the total memory for thelookuparray by using Binary search instead.
Here is first implementation
class Solution:
def maxValue(self, events: List[List[int]], k: int) -> int:
def sort_key_end(x):
return x[1]
def binary_search(arr, value):
l = -1
r = len(arr)
while l+1<r:
m = (l + r) //2
curr_val = arr[m]
if curr_val < value:
l = m
else:
r = m
is_found = l > -1
return is_found, l
events.sort(key=sort_key_end)
lookup = []
key = []
for index, (s, e, v) in enumerate(events):
lookup.append(v)
key.append(e)
is_found, possible = binary_search(key, s)
if is_found:
lookup[index] += lookup[possible]
if lookup[index] < lookup[index - 1]:
lookup[index] = lookup[index - 1]
return lookup[len(events)-1]
To check my (without k) implementation, the best match for this solution is 2008. Maximum Earnings From Taxi, the same question without k maximum number of events part but it isn’t inclusive thought, so I have to modify it a bit.
To add k into this solution, the best and easiest way is just store lookup by a matrix of n*k, where we add another dimension [0..k] on how much event we have attend. And update function into either:
- **(Case 1)** Last found best event `lookup[curr_attend][end] = lookup[curr_attend][end-1]`
- **(Case 2)** Choosing current event and best found `lookup[end_before]` with `end_before < start[index]` and have `curr_attend-1` total event had attended; or we can said `lookup[curr_attend][end] = value_of_current_event + lookup[curr_attend-1][start-1]`
class Solution:
def maxValue(self, events: List[List[int]], k: int) -> int:
def sort_key_end(x):
return x[1]
def binary_search(arr, value):
l = -1
r = len(arr)
while l+1<r:
m = (l + r) //2
curr_val = arr[m]
if curr_val < value:
l = m
else:
r = m
is_found = l > -1
return is_found, l
events.sort(key=sort_key_end)
lookup = [[] for _ in range(k)]
key = []
for index, (s, e, v) in enumerate(events):
key.append(e)
is_found, possible = binary_search(key, s)
for i in range(k):
lookup[i].append(v)
if is_found and i > 0:
lookup[i][index] += lookup[i-1][possible]
if lookup[i][index] < lookup[i][index - 1]:
lookup[i][index] = lookup[i][index - 1]
return lookup[k-1][len(events)-1]
Optimized:¶
We can use bisect instead of Binary searching, which is similar to Leetcode problem 2008. optimal solution. Where bisect_left(key, s) will find the index position of key array where key[bisect_left-1] < s <= key[bisect_left]
class Solution:
def maxValue(self, events: List[List[int]], k: int) -> int:
def sort_key_end(x):
return x[1]
events.sort(key=sort_key_end)
lookup = [[] for _ in range(k)]
key = []
for index, (s, e, v) in enumerate(events):
key.append(e)
search = bisect_left(key, s)
for i in range(k):
lookup[i].append(v)
if search > 0 and i > 0:
lookup[i][index] += lookup[i-1][search - 1]
if lookup[i][index] < lookup[i][index - 1]:
lookup[i][index] = lookup[i][index - 1]
return lookup[k-1][len(events)-1]
Best one yet?¶
Seem not, here is some thing else, where one try to implement a Python heap and a greedy approach:
- Start with the best possible event value till the lowest value.
Schedule()helper class- This is where we storing all event we had attend (
self.eventsarray) and total value of them (self.value). - This likely to keep track which set of event we currently chose (similar to our
lookupandkeyhelper array to store needed information dynamic programming ) - Each time we try to add a events, we create a new copy of it, so any modify is on a different array and don’t break previous found answer.
- This is where we storing all event we had attend (
- Main function store all solve
Schedule()object intoschedulesarray- With each
curr_event in eventswe try to either:- Push the event into a know
Schedule()solution - or Create a new
Schedule()solution branch with ourevents, this case to make sure there is a solution that had/possibly used thecurr_event(Even if it can be push out of heap in the end)
- Push the event into a know
- There is some try to check and update best possible answer within every schedules update loop (on the fly). Still double check it again (with the last for loop) before return the result
best
from typing import List import heapq class Schedule: def __init__(self, value=0, events=None): self.value = value self.events = [] if events is None else events def __lt__(self, other): return self.value < other.value or self.value == other.value and len(self.events) > len(other.events) def add_event(self, value, k): new_events = self.events.copy() new_value = self.value if k > len(new_events): new_events.append(value) new_value += value if k == len(new_events): heapq.heapify(new_events) elif value > new_events[0]: new_value += value - new_events[0] heapq.heapreplace(new_events, value) return Schedule(new_value, new_events) class Solution: def maxValue(self, events: List[List[int]], k: int) -> int: if k == 1: return max(e[2] for e in events) events = sorted(tuple(event) for event in events) best = Schedule() schedules = [] for start, end, value in events: okay = False while schedules and schedules[0][0] < start: e, s = heapq.heappop(schedules) heapq.heappush(schedules, (end, s.add_event(value, k))) if best < s: best = s okay = True if not okay: heapq.heappush(schedules, (end, best.add_event(value, k))) for e, s in schedules: if best < s: best = s return best.value
- With each
Final result¶
| Time Submitted | Status | Runtime | Memory | Language | Agro |
|---|---|---|---|---|---|
| 07/16/2023 01:02 | Accepted | 1046 ms | 62.7 MB | python3 | Binary search |
| 07/16/2023 01:01 | Accepted | 875 ms | 62.8 MB | python3 | Bisect optimized |
Created : August 16, 2023