2366. Minimum Replacements to Sort the Array

Problem¶

You are given a 0-indexed integer array nums. In one operation you can replace any element of the array with any two elements that sum to it.

For example, consider nums = [5,6,7]. In one operation, we can replace nums[1] with 2 and 4 and convert nums to [5,2,4,7].

Return the minimum number of operations to make an array that is sorted in non-decreasing order.

Example 1:

Input: nums = [3,9,3]
Output: 2
Explanation: Here are the steps to sort the array in non-decreasing order:

From [3,9,3], replace the 9 with 3 and 6 so the array becomes [3,3,6,3]
From [3,3,6,3], replace the 6 with 3 and 3 so the array becomes [3,3,3,3,3]
There are 2 steps to sort the array in non-decreasing order. Therefore, we return 2.

Example 2:

Input: nums = [1,2,3,4,5]
Output: 0
Explanation: The array is already in non-decreasing order. Therefore, we return 0.

Constraints:

1 <= nums.length <= 10**5
1 <= nums[i] <= 10**9

Solve¶

Thought on the problem¶

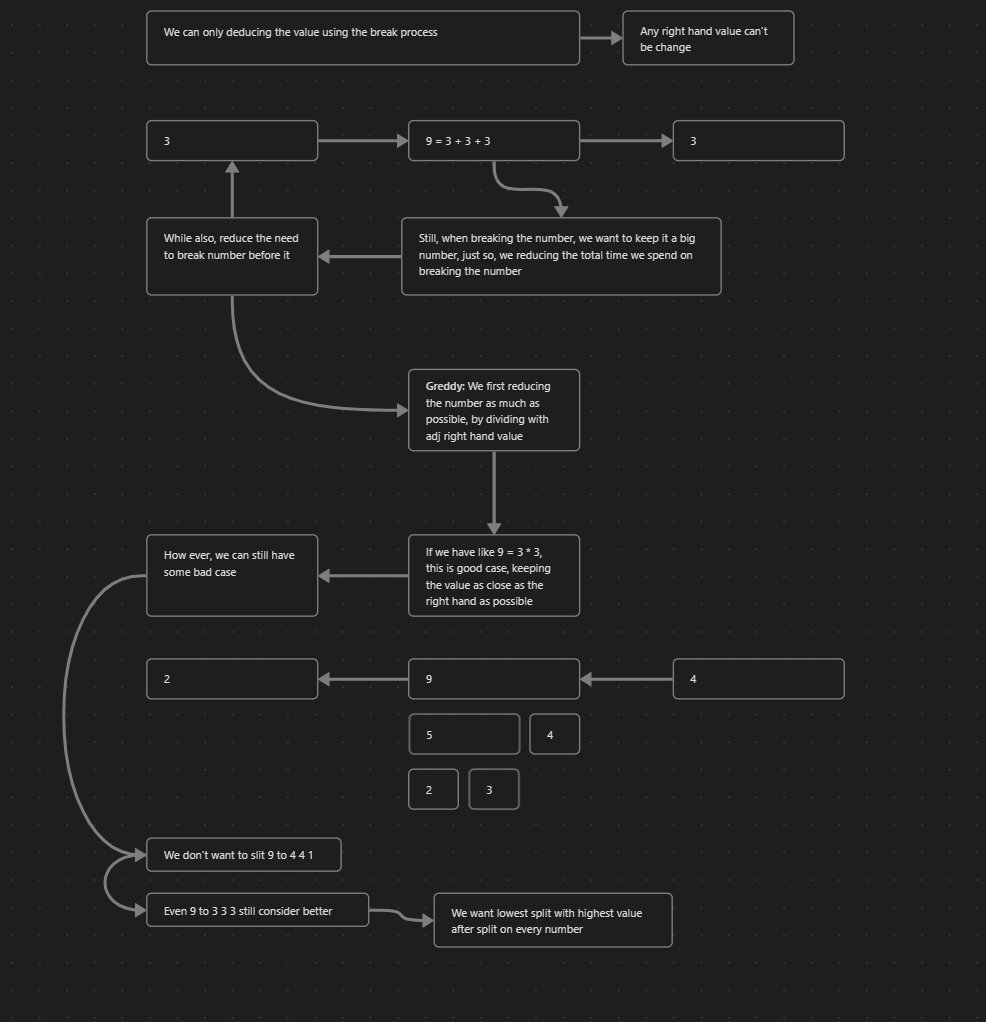
First analysis, I think greedy appear to be the best

2366. White board.canvas

Python - Greedy¶

class Solution:
    def minimumReplacement(self, nums: List[int]) -> int:
        cap = nums[-1]
        total = 0
        for i, curr in enumerate`-1]`:
            if i == 0:
                cap = curr
                continue
            if curr <= cap:
                cap = curr
                continue
            least_divison = curr // cap + int(curr % cap > 0)
            total += least_divison
            best = curr % least_divison
            if best == 0:
                best = least_divison
            cap = best
        return total

Let run it by hand, with input [2 9 4]

cap = 4, total = 0
loop (0, 4) => cap = 4
loop (1, 9) =>
- least_divison = 9 // 4 + int(9 % 4 > 0) = 2 + int (1 > 0) = 3
- total += 3 - 1 (to split 9 to 3 pieces, we only need 2 split)
- best = 9 % 3 = 0
- best == 0 => best = 3 (This seem wrong)
- cap = 3
loop (2, 2) => 2 < 3 => cap = 3
return total = 3 - 1

The first thing to fix is:

            total += (least_divison - 1)
            best = curr % least_divison ## What??
            if best == 0:
                best = curr // least_divison
            cap = best

We want the best split way, that split curr into least_divison piece that close together

(9, 3) => 3 3 3
(7, 2) => 4 3
(7, 3) => 2 2 3

To make it eaiser, using cap directly instead of least_divison

(10, 4) => 2 4 4 => 4 3 3
(29, 12) => 12 12 5 => 11 11 7 => 10 10 9 => 9 9 11

This can be achieve by

def split(x, cap):
    if x % cap == 0:
        return cap
    xmod = x % cap
    xdiv = x // cap
    minium = xmod
    eq = cap
    while minium < eq: 
        minium = minium + xdiv
        eq -= 1
    return min(eq, minium)

Test:
Hand run 1:

(29, 12)

- xmod = 5
- xdiv = 2
- minimum = 5
- eq = cap = 12
- (5 < 12) =>
    - minimum = 5 + 2 = 7
    - eq = 12 - 1 = 11
- (7 < 11) =>
    - minimum = 7 + 2 = 9
    - eq = 11 - 1 = 10
- (9 < 10) =>
    - minimum = 9 + 2 = 11
    - eq = 10 - 1 = 9
- (11 < 9) => End loop
- return min(11, 9) => return 9

Hand run 2:

(7, 4)

- xmod = 3
- xdiv = 1
- minimum = 3
- eq = 4
- (3 < 4) => 
    - minimum = 3 + 1 = 4
    - eq = 4 - 1 = 3
- return min(3,4) => return 3

Hand run 3:

(7, 6)

- xmod = 1
- xdiv = 1
- minimum = 1
- eq = 6
- (1 < 6) => 
    - minimum = 1 + 1 = 2
    - eq = 6 - 1 = 5
- (2 < 5) => 
- (3 < 4) => 
- (4 < 3) => 
- return min(3,4) => return 3

This can round down to one equation, this belong to to do list or just dividing it duh

Final implementation

Time Submitted	Status	Runtime	Memory	Language
08/30/2023 15:39	Accepted	507 ms	31.3 MB	python3

class Solution:
    def minimumReplacement(self, nums: List[int]) -> int:

        def split(x, cap):
            if x % cap == 0:
                return cap
            xmod = x % cap
            xdiv = x // cap
            minium = xmod
            eq = cap
            while minium < eq: 
                minium = minium + xdiv
                eq -= 1
            return min(eq, minium)

        cap = nums[-1]
        total = 0
        for i, curr in enumerate`-1]`:
            if i == 0:
                cap = curr
                continue
            if curr <= cap:
                cap = curr
                continue
            least_divison = curr // cap + int(curr % cap > 0)
            total += least_divison - 1
            cap = split(curr, cap)
        return total

Time complexity: O(n * ??)

First loop: O(n)
While loop with x mod and stuff: O( (cap - x % cap) // (x // cap + 1) ), which worst case should be 10 ** 9 (?); But cap always smaller than x, and by doing one round of maximum worst case will reduce cap greatly afterwards.

I found out it TLE with this input:

[999999999,1000000000,999999999]

Just use divide - (Turn out) it better¶

O(n)

We can split by just used division result, yeah, which do not thing on improving the run times

Time Submitted	Status	Runtime	Memory	Language
08/30/2023 16:14	Accepted	504 ms	31.1 MB	python3

class Solution:
    def minimumReplacement(self, nums: List[int]) -> int:
        cap = nums[-1]
        total = 0
        for i, curr in enumerate`-1]`:
            if i == 0:
                cap = curr
                continue
            if curr <= cap:
                cap = curr
                continue
            least_divison = curr // cap + int(curr % cap > 0)
            total += least_divison - 1
            cap = curr // least_divison
        return total

Last update : September 17, 2023
Created : September 3, 2023